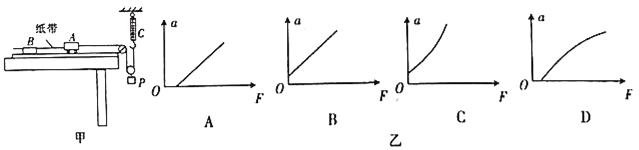
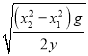题目内容
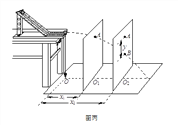
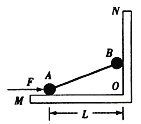
【题目】如图所示，在xOy平面的y轴左侧存在沿y轴正方向的匀强电场，y轴右侧区域I内存在垂直于纸面向内的匀强磁场，磁感应强度大小为
，区域II内有垂直纸面向外的匀强磁场，区域I、区域II的宽度均为
，高度分别为EF=2L，和DE= 
，质量也为m、电荷量为q的带正电的粒子从坐标为（-2L，-2L）的A点以速度
，沿x轴正方向射出，恰好经过坐标为（0，-L）的C点射入区域I，粒子重力忽略不计，求：
(1)匀强电场的电场强度大小E；
(2)要使粒子从区域II的右边界DE离开磁场，可在区域II内加垂直于纸面向外的匀强磁场，试确定磁感应强度B的大小范围；
(3)若粒子恰能从II区右边界DE间离x轴最远的点射出，求粒子在磁场中运动的时间。
【答案】(1) 
(2) 
(3) 
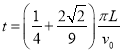
【解析】(1)带电粒子在匀强电场中做类平抛运动，有
， 
， 
， 
(2)设带电粒子经C典时的竖直分速度为
，速度为v， 
，解得
可知
方向与y轴正向成45°斜向上，粒子进入区域I做匀速圆周运动，
由
解得: 
根据几何关系可知，带电粒子从区域II的上边界离开磁场的半径满足
由
，
解得
(3)粒子在区域I磁场中转过的圆心角为
，
粒子在区域I区域运动的时间为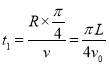
粒子在II区域运动的最大半径为r， 
转过的圆心角为β，由几何关系可知
粒子在区域II区域运动的时间为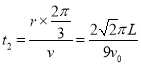
粒子在磁场中运动的时间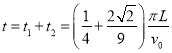
练习册系列答案
相关题目
