题目内容
【题目】如图所示,质量为mA=2Kg的物块A和质量为mB=4Kg的物块B紧挨着放置在粗糙的水平地面上,物块A的左侧连接一劲度系数为k=100N/m的轻质弹簧,弹簧另一端固定在竖直墙壁上。开始时两物块压缩弹簧并恰好处于静止状态,现使物块B在水平拉力F作用下向右做加速度为α=2m/s2,已知两物块与地面间的动摩擦因数均为μ=0.5,下列说法正确的是()
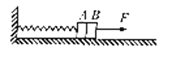
A. 因为物块B做匀加速直线运动,所以拉力F是恒力
B. 拉力F的最大值为Fmax=38N
C. 物块B与物块A分离时弹簧处于伸长状态,其伸长量为x=6cm
D. 物块B与物块A分离时弹簧处于压缩状态,其压缩量为x=14cm
【答案】D
【解析】A与B没有分离时,以整体为研究对象,可知整体受到重力、地面的支持力、弹簧的弹力、地面的摩擦力以及拉力F的作用,沿水平方向:F+kx-f=(mA+mB)a;f是滑动摩擦力,与物体的速度大小无关,在滑动的过程中不变;由于随A、B向右运动的过程中弹簧的压缩量x减小,所以F需逐渐增大,选项A错误。当弹簧的压缩量为x=0时,F最大,最大值为Fmax =(mA+mB)a+μ(mA+mB)g=42N,选项B错误;以A为研究对象,当B与A分离时,A的加速度与B的加速度是相等的,此时A受到弹簧的弹力与地面的摩擦力,由于摩擦力的方向向左,所以A必定受到弹簧需要的弹力,弹簧仍然处于压缩状态;由牛顿第二定律,对A:kx-μmAg=mAa;所以: ![]() ,故C错误,D正确。故选D。
,故C错误,D正确。故选D。

练习册系列答案
相关题目