题目内容

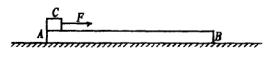
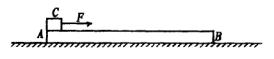
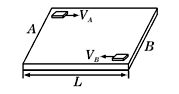
如图所示，长L＝1m的木板M静止在光滑水平面上，在其左右两端分别有小滑块A和B，质量分别为、，滑块与木板间的动摩擦因数，欲使A、B分别以速度和相向运动，直至A到板的右端，B到达板的左端，要求A和B滑块不掉下木板，且初功能之和有最小值，试求和各为多少？

   

   


解析:

由题意要求可知，滑块A、B和木板M三者都相对静止，且有共同速度，对系统由动量守恒得（取的方向为正方向）

                   ①

由能量守恒有：

      ②

欲使A和B两滑块的初动能最小，只有A、B、M三者共同速度才可满足，因此，当A、B、M三者最后均静止时，A与B的初动能之和为最小。则①②式可变为：

                   （3）

          （4）

代入数据解（3）（4）得：

   

练习册系列答案
相关题目

如图所示，长L＝1m，质量M＝1kg的木板AB静止在光滑的水平面上．在木板的最左端A处有一个质量m＝1kg的小物体C静止在木板上．现用F＝20N的水平恒力作用于物体C上，使它由静止开始向右运动．已知C与木板间滑动摩擦因数μ＝0.5，g＝10m/s2．求物体C由A端运动到B端时，水平恒力对物体C所做的功及物体C、木板AB速度各是多少？

如图所示，长L＝1m，质量M＝1kg的木板AB静止在光滑的水平面上．在木板的最左端A处有一个质量m＝1kg的小物体C静止在木板上．现用F＝20N的水平恒力作用于物体C上，使它由静止开始向右运动．已知C与木板间滑动摩擦因数m ＝0.5，．求物体C由A端运动到B端时，水平恒力对物体C所做的功及物体C、木板AB速度各是多少?

 
如图所示，长L＝1m，质量M＝1kg的木板AB静止在光滑的水平面上．在木板的最左端A处有一个质量m＝1kg的小物体C静止在木板上．现用F＝20N的水平恒力作用于物体C上，使它由静止开始向右运动．已知C与木板间滑动摩擦因数m ＝0.5，．求物体C由A端运动到B端时，水平恒力对物体C所做的功及物体C、木板AB速度各是多少?

 

如图所示，长S＝10m的平台AB固定，长L=6m质量M=3kg的木板放在光滑地面上，与平台平齐且靠在B处，右侧有落差h=0.1m的光滑弧形桥CD（桥的支柱未画出），桥面的最低位置与AB水平线等高（木板可从桥下无障碍的前行）。已知木板右侧与弧形桥左侧C端的水平距离d=1.5m，弧形桥顶部圆弧半径相等R=0.4m（半径未画出）。现有质量m=1kg的物块，以初速度v0=12m/s从A点向右运动，过B点后滑上木板，物块与平台、木板间的滑动摩擦因数 μ＝0.4，物块滑上弧形桥时无机械能损失，当物块到达圆弧最高点时D时，木板中点刚好到达D点正下方。物块大小忽略，重力加速度g=10m/s2。求：

（1）物块滑至B点时的速度大小v；

（2）物块与木板能否达到共速，若能，确定两物体共速时木板的位置和物块在木板上的位置；

（3）物块到达弧形桥顶端D点时所受到的支持力F及物块与木板相碰点到木板左端的距离S0.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网