题目内容
【题目】如图所示，圆盒为电子发射器，M处是电子出射口。其正视截面如图所示，D为绝缘外壳，整个装置处于真空中，半径为R的金属圆柱的圆心A处有一离子源，可沿半径向外均匀发射速率为v的低能电子，与金属圆柱同轴放置的金属网C的半径为3R。不需要电子射出时，可用磁场将电子封闭在金属网以内；若需要低能电子射出时，可撤去磁场，让电子直接射出；若需要高能电子，撤去磁场，并在金属圆柱A和金属网C间加一径向电场，使其加速后射出。不考虑金属圆柱A和金属网C的静电感应电荷对电子的作用和电子之间的相互作用，忽略电子的重力，已知电子质量为m，电荷最为e。
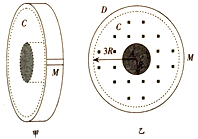
(1)若需要速度为3v的电子通过金属网C发射出来，在金属圆柱A和金属网C间所加电压U是多大；
(2)若金属圆柱A和金属网C间不加电压，要使由金属圆柱A发射的电子不从金属网C射出，可在金属网内环形区域加垂直于圆盒平面向外的匀强磁场，则所加磁场磁感应强度B应满足什么条件。
【答案】（1）
（2）
【解析】
（1）电子经AC间的电场加速时，由动能定理得：eU＝
m(3v)2mv2
所需加速电压为：U＝
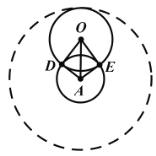
（2）电子在AC间磁场中做匀速圆周运动，其轨迹圆与金属网相切时，磁感应强度B有最小值。设此轨迹圆的半径为r，则有：Bev＝m
由几何关系得：（3R-r）2=r2+R2
解得：r＝
R
最小磁感应强度为：B＝
则所加磁场磁感应强度B应满足：
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
