题目内容
6.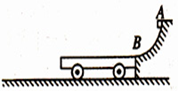 如图所示,AB为半径R=0.8m的$\frac{1}{4}$光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3kg,车长L=2.06m,车上表面距地面的高度h=0.2m.现有一质量m=lkg的小滑块(可看成质点),由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求:
如图所示,AB为半径R=0.8m的$\frac{1}{4}$光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3kg,车长L=2.06m,车上表面距地面的高度h=0.2m.现有一质量m=lkg的小滑块(可看成质点),由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求:(1)滑块到达B端时,轨道对它支持力的大小
(2)车被锁定时,车右端距轨道B端的距离
(3)从车开始运动到被锁定的过程中,滑块与车面间由于摩擦而产生的内能大小
(4)滑块落地点离车左端的水平距离.
分析 (1)由机械能守恒定律求出滑块到B端的速度,由牛顿第二定律求出支持力.
(2)根据牛顿第二定律分别求出滑块和小车的加速度,由运动式求出两者速度相同经过的时间,确定两者的运动情况.再求解车右端距轨道B端的距离.
(3)求出滑块相对于小车的位移△x,由内能E=μmg△x求出内能.
(4)滑块滑出小车后做平抛运动,求出滑块滑到A端的速度和平抛的时间,求解滑块落地点离车左端的水平距离.
解答 解:(1)设滑块到达B端时速度为v,由机械能守恒定律,得:mgR=$\frac{1}{2}m{v}^{2}$
由牛顿第二定律,得:FN-mg=$m\frac{{v}^{2}}{R}$
联立两式,代入数值解得:FN=3mg=30N.
(2)当滑块滑上小车后,由牛顿第二定律,得
对滑块有:-μmg=ma1
对小车有:μmg=Ma2
设经时间t两者达到共同速度,则有:v+a1t=a2t
解得:t=1 s.
由于1 s<1.5 s,此时小车还未被锁定,两者的共同速度:v′=a2t=1 m/s 两者一起匀速运动,直到小车被锁定.
故车被锁定时,车右端距轨道B端的距离:x=$\frac{1}{2}{a}_{2}{t}^{2}+v′t′$,
代入数据解得:x=1 m.
(3)从车开始运动到被锁定的过程中,滑块相对小车滑动的距离为:$△x=\frac{v+v′}{2}t-\frac{1}{2}{a}_{2}{t}^{2}$=2 m
故产生的内能:E=μmg△x=0.3×10×2J=6 J.
(4)对滑块由动能定理,得:-μmg(L-△x)=$\frac{1}{2}mv{″}^{2}-\frac{1}{2}mv{′}^{2}$
滑块脱离小车后,在竖直方向有:h=$\frac{1}{2}gt{″}^{2}$
代入数据得,滑块落地点离车左端的水平距离:x′=v″t″=0.16 m.
答:(1)滑块到达B端时,轨道对它支持力的大小为30N.
(2)车被锁定时,车右端距轨道B端的距离为1m.
(3)从车开始运动到被锁定的过程中,滑块与车面间由于摩擦而产生的内能大小为6J.
(4)滑块落地点离车左端的水平距离为0.16m.
点评 本题之处在于分析滑块和小车速度相同所经历的时间,与1.5s进行比较来分析两者的运动情况.求摩擦生热Q=f△x,△x是相对位移.

| A. |  电子束通过铝箔时的衍射图样证实了电子具有粒子性 | |
| B. | 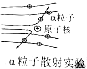 发现少数α粒子发生了较大偏转,说明原子的质量绝大部分集中在很小空间范围 | |
| C. |  根据玻尔理论,氢原子的轨道半径是任意的 | |
| D. | 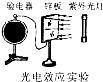 光电效应实验说明光具有粒子性 |
| A. | $\frac{F}{4}$ | B. | F | C. | 4F | D. | 16F |
| A. | 式中k值,对所有行星和卫星都相等 | |
| B. | 围绕不同恒星运行的行星,其k值一般不同 | |
| C. | 公式只适用于绕太阳做椭圆轨道运行的行星 | |
| D. | 公式适用于宇宙中所有围绕恒星运动的行星 |
 如图a、b所示,分别用等大的拉力F作用在同一物体上,使物体沿水平面向右运动相同的位移s.a中拉力F水平向右,水平面光滑,拉力F做功为Wa,b中拉力F斜向右上方,与水平方向间的夹角为α,物体与水平面间有摩擦力,拉力F做功为Wb,则( )
如图a、b所示,分别用等大的拉力F作用在同一物体上,使物体沿水平面向右运动相同的位移s.a中拉力F水平向右,水平面光滑,拉力F做功为Wa,b中拉力F斜向右上方,与水平方向间的夹角为α,物体与水平面间有摩擦力,拉力F做功为Wb,则( )| A. | Wa=Wb | B. | Wa<Wb | ||
| C. | Wa>Wb | D. | 以上三种情况都有可能 |
| A. | 该星球的密度是地球密度的2倍 | |
| B. | 该星球表面的重力加速度是地球表面重力加速度的4倍 | |
| C. | 该星球的近地卫星的速度是地球近地卫速度的4倍 | |
| D. | 该星球的近地卫星周期跟地球的近地卫星周期相等 |
 在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下:
在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下: 如图所示,一轻质弹簧下端固定,直立于水平地面上,将质量为m的物体A从离弹簧顶端正上方h高处由静止释放,当物体A下降到最低点P时,其速度变为零,此时弹簧的压缩量为x0;若将质量为3m的物体B从离弹簧顶端正上方同一h高处,由静止释放,当物体B也下降到P处时,其动能为( )
如图所示,一轻质弹簧下端固定,直立于水平地面上,将质量为m的物体A从离弹簧顶端正上方h高处由静止释放,当物体A下降到最低点P时,其速度变为零,此时弹簧的压缩量为x0;若将质量为3m的物体B从离弹簧顶端正上方同一h高处,由静止释放,当物体B也下降到P处时,其动能为( )