题目内容
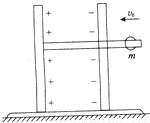 如图,电容器同定在一个绝缘座上,绝缘座放在光滑水平面上,平行板电容器板间距离为d,右极板有一小孔,通过孔有一绝缘杆,左端固定在左极板上,电容器极板连同底座、绝缘杆总质景为M.给电容器充电后,有一质最为m的带正电环恰套在杆上以某一初速度V对准小孔向左运动,设带电环不影响电容器板间电场的分布.带电环进入电容器后距左板的最小距离为的d/3,则带电环与左极扳相距最近时的速度v= ,过程中系统增加的电势能最大值为 .
如图,电容器同定在一个绝缘座上,绝缘座放在光滑水平面上,平行板电容器板间距离为d,右极板有一小孔,通过孔有一绝缘杆,左端固定在左极板上,电容器极板连同底座、绝缘杆总质景为M.给电容器充电后,有一质最为m的带正电环恰套在杆上以某一初速度V对准小孔向左运动,设带电环不影响电容器板间电场的分布.带电环进入电容器后距左板的最小距离为的d/3,则带电环与左极扳相距最近时的速度v= ,过程中系统增加的电势能最大值为 .
【答案】分析:选取带电环与电容器作为研究对象,根据动量守恒定律,即可求出带电环与左极扳相距最近时的速度大小;再由动能定理,可求出此过程中系统电势能的增加量.
解答:解:选取带电环与电容器作为研究对象,设相距最近时速度大小为v,
根据动量守恒定律,则有mv=(m+M)v
解得:v=
在运动过程中,根据动能定理,
则有:W=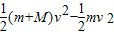
电场力做负功,导致电势能增加,
则电势能的增加量,为△E=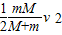
故答案为: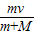 ;
;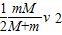 .
.
点评:考查动量守恒定律与动能定理的应用,注意动量守恒定律的守恒条件与方向性,并掌握动能定理的功的正负.
解答:解:选取带电环与电容器作为研究对象,设相距最近时速度大小为v,
根据动量守恒定律,则有mv=(m+M)v
解得:v=

在运动过程中,根据动能定理,
则有:W=
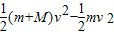
电场力做负功,导致电势能增加,
则电势能的增加量,为△E=
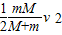
故答案为:
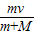 ;
;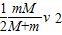 .
.点评:考查动量守恒定律与动能定理的应用,注意动量守恒定律的守恒条件与方向性,并掌握动能定理的功的正负.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 如图所示是电动势随时间按正弦波和三角波变化的波形图,下列关于这两种波形的说法正确的是( )
如图所示是电动势随时间按正弦波和三角波变化的波形图,下列关于这两种波形的说法正确的是( )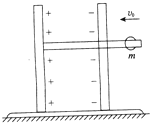 如图,电容器同定在一个绝缘座上,绝缘座放在光滑水平面上,平行板电容器板间距离为d,右极板有一小孔,通过孔有一绝缘杆,左端固定在左极板上,电容器极板连同底座、绝缘杆总质景为M.给电容器充电后,有一质最为m的带正电环恰套在杆上以某一初速度V0对准小孔向左运动,设带电环不影响电容器板间电场的分布.带电环进入电容器后距左板的最小距离为的d/3,则带电环与左极扳相距最近时的速度v=
如图,电容器同定在一个绝缘座上,绝缘座放在光滑水平面上,平行板电容器板间距离为d,右极板有一小孔,通过孔有一绝缘杆,左端固定在左极板上,电容器极板连同底座、绝缘杆总质景为M.给电容器充电后,有一质最为m的带正电环恰套在杆上以某一初速度V0对准小孔向左运动,设带电环不影响电容器板间电场的分布.带电环进入电容器后距左板的最小距离为的d/3,则带电环与左极扳相距最近时的速度v=
