题目内容
8.为了减少光在透镜表面的损失,可以在透镜表面涂上一层增透膜,一般用折射率为n的氟化镁,为了使波长为λ的绿光在垂直表面入射时反射光能量足够小,试计算:(1)绿光在透镜中传播的波长是多少?
(2)所涂薄膜的厚度至少是多少?
分析 (1)根据n=$\frac{c}{v}$,结合c=λf,即可求解;
(2)根据最小厚度为绿光在膜中波长的$\frac{1}{4}$,结合第(1)结论,即可求解.
解答 解:由于人眼对绿光最敏感,所以通常所用的光学仪器其镜头表面所涂的增透膜的厚度只使反射的绿光干涉相消,
但薄膜的厚度不宜过大,只需使其厚度为绿光在膜中波长的$\frac{1}{4}$,使绿光在增透膜的前、后两个表面上的反射光互相抵消.
而光从真空进入某种介质后,其波长会发生变化.
若绿光在真空中波长为λ,在增透膜中的波长为λ′,由折射率与光速的光系和光速与波长及频率的关系得:
n=$\frac{c}{v}$=$\frac{λf}{λ′f}$,
得:λ′=$\frac{λ}{n}$,
那么增透膜厚度为:d=$\frac{1}{4}λ′$=$\frac{λ}{4n}$
答:(1)绿光在透镜中传播的波长是$\frac{λ}{n}$;
(2)所涂薄膜的厚度至少是$\frac{λ}{4n}$.
点评 本题考查了光的干涉,知道波程差为半波长的奇数倍时为减弱点,注意公式n=$\frac{c}{v}$,结合c=λf,及理解最小厚度的要求.

练习册系列答案
相关题目
10.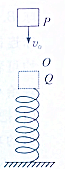 如图所示,质量m=2kg的小物块,从某高处光滑P点以v0=5m/s的初速度抛下,在O点与竖直弹簧接触压缩到Q点时速度为零,P,Q的竖直高度是5m,P,O的高度为4.5m,如果选取Q点所在的水平面为重力势能的零势能面,则物体从P到Q的过程中( )
如图所示,质量m=2kg的小物块,从某高处光滑P点以v0=5m/s的初速度抛下,在O点与竖直弹簧接触压缩到Q点时速度为零,P,Q的竖直高度是5m,P,O的高度为4.5m,如果选取Q点所在的水平面为重力势能的零势能面,则物体从P到Q的过程中( )
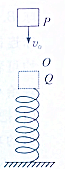 如图所示,质量m=2kg的小物块,从某高处光滑P点以v0=5m/s的初速度抛下,在O点与竖直弹簧接触压缩到Q点时速度为零,P,Q的竖直高度是5m,P,O的高度为4.5m,如果选取Q点所在的水平面为重力势能的零势能面,则物体从P到Q的过程中( )
如图所示,质量m=2kg的小物块,从某高处光滑P点以v0=5m/s的初速度抛下,在O点与竖直弹簧接触压缩到Q点时速度为零,P,Q的竖直高度是5m,P,O的高度为4.5m,如果选取Q点所在的水平面为重力势能的零势能面,则物体从P到Q的过程中( )| A. | 合力对物块做的功是-25J | B. | 物块的机械能守恒 | ||
| C. | 物块克服弹簧的弹力做的功是125J | D. | 物块的最大动能是110J |
19.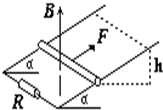 如图所示,两根光滑的金属导轨,平行放置在倾角为α的斜面上,导轨的下端接有电阻R,导轨自身的电阻不计,整个装置处在一方向垂直地面向上的匀强磁场中.质量为m,电阻不计的金属棒ab垂直两导轨,在方向沿斜面向上且与金属棒垂直的恒力F作用下沿导轨匀速上行,那么在它升高了h的过程中( )
如图所示,两根光滑的金属导轨,平行放置在倾角为α的斜面上,导轨的下端接有电阻R,导轨自身的电阻不计,整个装置处在一方向垂直地面向上的匀强磁场中.质量为m,电阻不计的金属棒ab垂直两导轨,在方向沿斜面向上且与金属棒垂直的恒力F作用下沿导轨匀速上行,那么在它升高了h的过程中( )
 如图所示,两根光滑的金属导轨,平行放置在倾角为α的斜面上,导轨的下端接有电阻R,导轨自身的电阻不计,整个装置处在一方向垂直地面向上的匀强磁场中.质量为m,电阻不计的金属棒ab垂直两导轨,在方向沿斜面向上且与金属棒垂直的恒力F作用下沿导轨匀速上行,那么在它升高了h的过程中( )
如图所示,两根光滑的金属导轨,平行放置在倾角为α的斜面上,导轨的下端接有电阻R,导轨自身的电阻不计,整个装置处在一方向垂直地面向上的匀强磁场中.质量为m,电阻不计的金属棒ab垂直两导轨,在方向沿斜面向上且与金属棒垂直的恒力F作用下沿导轨匀速上行,那么在它升高了h的过程中( )| A. | 作用于金属棒上各力的合力所做的功等于零 | |
| B. | 恒力F与安培力的合力所做的功等于零 | |
| C. | 恒力F与重力G的合力所做的功等于电阻R上的焦耳热 | |
| D. | 作用于金属棒上各力的合力所做的功等于mgh与电阻R上的焦耳热之和 |
16. 小球A质量为2kg,斜面体B的质量为10kg,斜面倾角θ=30°,已知 A、B间和B与地面之间的动摩擦因数均为?=0.27,将物体A放在斜面B上端的同时,给B施加一水平力F,为使A沿竖直方向落地,拉力F的大小至少为( )
小球A质量为2kg,斜面体B的质量为10kg,斜面倾角θ=30°,已知 A、B间和B与地面之间的动摩擦因数均为?=0.27,将物体A放在斜面B上端的同时,给B施加一水平力F,为使A沿竖直方向落地,拉力F的大小至少为( )
 小球A质量为2kg,斜面体B的质量为10kg,斜面倾角θ=30°,已知 A、B间和B与地面之间的动摩擦因数均为?=0.27,将物体A放在斜面B上端的同时,给B施加一水平力F,为使A沿竖直方向落地,拉力F的大小至少为( )
小球A质量为2kg,斜面体B的质量为10kg,斜面倾角θ=30°,已知 A、B间和B与地面之间的动摩擦因数均为?=0.27,将物体A放在斜面B上端的同时,给B施加一水平力F,为使A沿竖直方向落地,拉力F的大小至少为( )| A. | 200N | B. | 100N | C. | 100$\sqrt{3}$N | D. | 200$\sqrt{2}$N |
3.如图所示为甲、乙两物体从同一地点沿直线向同一方向运动的v-t图象,则( )
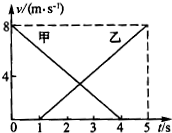

| A. | 甲、乙两物体在4s末相距最远 | B. | 甲、乙两物体在2.5s末相距最近 | ||
| C. | 甲、乙两物体在5s末相遇 | D. | 前4s内甲物体总在乙的前面 |
13.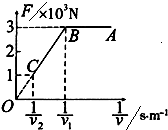 一辆汽车质量为1×103 kg,最大功率为2×104W,在水平路面上由静止开始做直线运动,最大速度为υ2,运动中汽车所受阻力恒定.发动机的最大牵引力为3×103N,其行驶过程中牵引力F与车速的倒数$\frac{1}{v}$的关系如图所示.下列判断错误的是( )
一辆汽车质量为1×103 kg,最大功率为2×104W,在水平路面上由静止开始做直线运动,最大速度为υ2,运动中汽车所受阻力恒定.发动机的最大牵引力为3×103N,其行驶过程中牵引力F与车速的倒数$\frac{1}{v}$的关系如图所示.下列判断错误的是( )
 一辆汽车质量为1×103 kg,最大功率为2×104W,在水平路面上由静止开始做直线运动,最大速度为υ2,运动中汽车所受阻力恒定.发动机的最大牵引力为3×103N,其行驶过程中牵引力F与车速的倒数$\frac{1}{v}$的关系如图所示.下列判断错误的是( )
一辆汽车质量为1×103 kg,最大功率为2×104W,在水平路面上由静止开始做直线运动,最大速度为υ2,运动中汽车所受阻力恒定.发动机的最大牵引力为3×103N,其行驶过程中牵引力F与车速的倒数$\frac{1}{v}$的关系如图所示.下列判断错误的是( )| A. | 汽车先做匀速运动,再做加速运动 | |
| B. | 最大速度大小为20m/s | |
| C. | 整个过程中最大加速度为2m/s2 | |
| D. | 汽车速度为10m/s时发动机的功率为20kW |
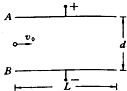 如图所示,质量为m,电荷量为q的微粒以某一速度从两极板正中间入射,若两板不加电压,微粒刚好能从B板边缘飞出,加如图方向的电压后,粒子刚好能从A板边缘飞出,已知极板长L,间距为d,重力加速度为g,求:
如图所示,质量为m,电荷量为q的微粒以某一速度从两极板正中间入射,若两板不加电压,微粒刚好能从B板边缘飞出,加如图方向的电压后,粒子刚好能从A板边缘飞出,已知极板长L,间距为d,重力加速度为g,求: 如图所示,离地面高H=40cm处的水平轴上装有均匀杆.杆长L=30cm,质量M=0.5kg,杆偏离竖直方向α=30°,靠在地面上半径r=10cm的球上,整个系统处于平衡状态,则球与地面间的摩擦力为0.75N,球与杆的摩擦力为0.75N.
如图所示,离地面高H=40cm处的水平轴上装有均匀杆.杆长L=30cm,质量M=0.5kg,杆偏离竖直方向α=30°,靠在地面上半径r=10cm的球上,整个系统处于平衡状态,则球与地面间的摩擦力为0.75N,球与杆的摩擦力为0.75N.