题目内容
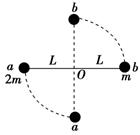
如图14所示,水平转盘的中心有一个光滑的竖直小圆筒,质量为m的物体A放在转盘上,A到圆心的距离为r,物体A通过轻绳与物体B相连,B与A质量相同.若物体A与转盘间的动摩擦因数为μ,则转盘转动的角速度ω在什么范围内,物体A才能随盘转动?
图14
解析:当A将要沿圆盘向外滑动时,A所受的最大静摩擦力指向圆心,此时A做圆周运动所需的向心力为绳的拉力与最大静摩擦力的合力,即F+Ffm=mrω12①
由于B静止,则F=mg②
又因为Ffm=μFN=μmg③
由①②③式可解得:ω1=![]()
当A要沿圆盘向圆心滑动时,A所受的最大静摩擦力沿半径向外,这时向心力为:
F-Ffm=mrω22④
由②③④式可解得:ω2=![]()
故要使A随圆盘一起转动,其角速度应满足![]() ≤ω≤
≤ω≤![]() .
.
答案:![]() ≤ω≤
≤ω≤![]()

练习册系列答案
相关题目