题目内容
在遥远的某类似太阳系的恒星系中,据观察发现,观察到的行星绕行方向都一致,且均在同一平面内。现发现行星A离该恒星的距离为R,围绕恒星运动的周期为T,该行星做近似圆周运动,但每隔2T其半径就有微小增加,然后回复原值。科学家猜测其附近应该还有一颗行星,请你根据这些条件判断:这颗未知行星处于行星A的内侧还是外侧?距恒星的距离为多少?
解:因为每隔一定时间,A行星半径就增大一点,说明受到外侧的引力,所以未知行星B应位于行星A的外侧
两行星均做圆周运动,每隔2T相距最近,因内侧行星角速度较大,再次相距最近时A行星多转了2π角度,而总时间相等
ωA·2T-ωB·2T=2π
ωA=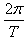 ,ωB=
,ωB=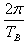
得:TB=2T
由万有引力定律可知: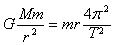
所以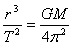 ,即
,即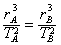 ,解得:
,解得: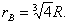
两行星均做圆周运动,每隔2T相距最近,因内侧行星角速度较大,再次相距最近时A行星多转了2π角度,而总时间相等
ωA·2T-ωB·2T=2π
ωA=
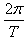 ,ωB=
,ωB=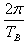
得:TB=2T
由万有引力定律可知:
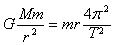
所以
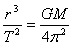 ,即
,即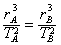 ,解得:
,解得: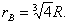

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目