题目内容
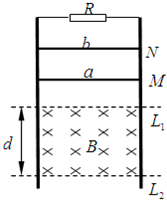如图所示，电阻忽略不计的、两根平行的光滑金属导轨竖直放置，其上端接一阻值为3Ω的定值电阻R．在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B、磁场区域的高度为d=0.5m．导体棒a的质量ma=0.2kg，电阻Ra=3Ω；导体棒b的质量mb=0.1kg，电阻Rb=6Ω．它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动，且都能匀速穿过磁场区域，当b刚穿出磁场时a正好进入磁场．设重力加速度为g=10m/s2．（不计a、b之间的作用，整个运动过程中a、b棒始终与金属导轨接触良好）求：（1）在整个过程中a、b两棒克服安培力分别做的功；
（2）a进入磁场的速度与b进入磁场的速度之比：
（3）分别求出M点和N点距虚线L1的高度．
分析：（1）a、b在磁场中匀速运动，其安培力等于各自的重力，根据重力做功情况求出a、b两棒克服安培力分别做的功．
（2）a、b进入磁场都做匀速直线运动，受重力和安培力平衡，根据平衡，结合闭合电路欧姆定律和切割产生感应电动势大小公式，求出a、b做匀速直线运动的速度大小，从而求出两速度之比．
（3）根据a、b棒进入磁场中的速度之比，通过位移公式求出M点和N点距虚线L1的高度之比，抓住当b刚穿出磁场时a正好进入磁场，有va=vb+gt，d=vbt结合a、b的速度比，求出M点和N点距虚线L1的高度．
（2）a、b进入磁场都做匀速直线运动，受重力和安培力平衡，根据平衡，结合闭合电路欧姆定律和切割产生感应电动势大小公式，求出a、b做匀速直线运动的速度大小，从而求出两速度之比．
（3）根据a、b棒进入磁场中的速度之比，通过位移公式求出M点和N点距虚线L1的高度之比，抓住当b刚穿出磁场时a正好进入磁场，有va=vb+gt，d=vbt结合a、b的速度比，求出M点和N点距虚线L1的高度．
解答：解：（1）因a、b在磁场中匀速运动，其安培力等于各自的重力，由功的公式得
Wa=magd=1.0 J
Wb=mbgd=0.5J
（2）b在磁场中匀速运动时：速度为vb，总电阻R1=7.5Ω
b中的电流Ib=
①
=mbg ②
同理，a棒在磁场中匀速运动时：速度为va，总电阻R2=5Ω：
=mag ③
由以上各式得：
=
④
（3）v2=2gh ⑤
=
⑥
va=vb+gt ⑦
d=vbt ⑧
由④⑤⑥⑦⑧得ha=
m=1.33 m
hb=
m=0.75 m
答：（1）在整个过程中a、b两棒克服安培力分别做的功为1J、0.5J．
（2）a进入磁场的速度与b进入磁场的速度之比为4：3．
（3）M点和N点距虚线L1的高度分别为1.33m、0.75m．
Wa=magd=1.0 J
Wb=mbgd=0.5J
（2）b在磁场中匀速运动时：速度为vb，总电阻R1=7.5Ω
b中的电流Ib=
| BLvb |
| R1 |
| B2L2vb |
| R1 |
同理，a棒在磁场中匀速运动时：速度为va，总电阻R2=5Ω：
| B2L2va |
| R2 |
由以上各式得：
| vb |
| va |
| 3 |
| 4 |
（3）v2=2gh ⑤
| hb |
| ha |
| 9 |
| 16 |
va=vb+gt ⑦
d=vbt ⑧
由④⑤⑥⑦⑧得ha=
| 4 |
| 3 |
hb=
| 3 |
| 4 |
答：（1）在整个过程中a、b两棒克服安培力分别做的功为1J、0.5J．
（2）a进入磁场的速度与b进入磁场的速度之比为4：3．
（3）M点和N点距虚线L1的高度分别为1.33m、0.75m．
点评：解决本题的关键知道导体棒做匀速直线运动时，重力和安培力平衡，本题的难点在于通过a、b棒的速度关系以及a、b距离虚线L1的高度比求出a、b距离虚线L1的高度．
练习册系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
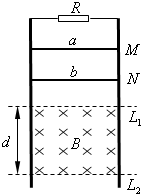如图所示，电阻忽略不计的两根两平行光滑金属导轨竖直放置，其上端接一阻值为3Ω的电阻R．在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B，磁场区域的高度为d=0.5m．导体棒a的质量ma=0.2kg、电阻Ra=3Ω；导体棒b的质量mb=0.1kg、电阻Rb=6Ω，它们分别从图中M、N处同时由静止开始沿导轨向下滑动，且都能匀速穿过磁场区域，当b 刚穿出磁场时a正好进入磁场．（不计a、b之间的作用）求：
如图所示，电阻忽略不计的光滑导轨AB、CD相距0.5m平行放置，其长度足够长，AB、CD组成的平面与水平面成30°角．垂直于ABCD平面斜向下的匀强磁场的磁感应强度B=1T，电源电动势E=2V、内阻r=1Ω，R1=2Ω，金属杆MN的电阻R2=2Ω．闭合电键S后，MN恰好静止在斜面上．g=10m/s2．求：
（2009?盐城模拟）如图所示，电阻忽略不计的、两根两平行的光滑金属导轨竖直放置，其上端接一阻值为3Ω的定值电阻R．在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B，磁场区域的高度为d=0.5m．导体棒a的质量ma=0.2kg、电阻Ra=3Ω；导体棒b的质量mb=0.1kg、电阻Rb=6Ω，它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动，且都能匀速穿过磁场区域，当b 刚穿出磁场时a正好进入磁场． 设重力加速度为g=10m/s2．（不计a、b之间的作用）求：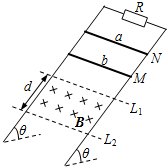
如图所示，电阻忽略不计的两根平行光滑的金属杆构成的导轨倾斜放置，导轨平面与水平面间夹角θ=37°，导轨上端接一阻值为3Ω的电阻R．在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B，L1、L2间的距离为d=0.5m．导体棒a的质量ma=0.2kg、电阻Ra=3Ω；导体棒b的质量mb=0.1kg、电阻Rb=6Ω，它们分别从图中M、N处同时由静止开始沿导轨向下滑动，且都能匀速穿过磁场区域，当b 刚穿出磁场时a正好进入磁场．（不计a、b之间的作用，g取10m/s2）求：