题目内容
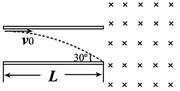
长为L的平行金属板水平放置,两极板带等量的异种电荷,板间形成匀强电场,平行金属板的右侧有如下图所示的匀强磁场。一个带电为+q、质量为m的带电粒子,以初速v0紧贴上板垂直于电场线方向进入该电场,刚好从下板边缘射出,射出时末速度恰与下板成30o角,出磁场时刚好紧贴上板右边缘,不计粒子重力 ,求:
,求:
小题1:两板间的距离;
小题2:匀强电场的场强与匀强磁场的磁感应强度。
 ,求:
,求:小题1:两板间的距离;
小题2:匀强电场的场强与匀强磁场的磁感应强度。

小题1:
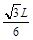
小题2:
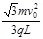
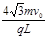
(1)带电粒子在电场中受到电场力的作用发生偏转,做类平抛运动。
竖直方向:离开电场时的速度vy=v0tan30°(1分)粒子发生偏转的位移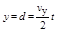 (1分)
(1分)
水平方向:粒子匀速运动的时间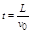 (1分)联立以上几式解得,
(1分)联立以上几式解得,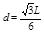 (1分)
(1分)
(2)在电场中粒子受到电场力,由牛顿第二定律得,qE=ma(1分)
根据运动学公式有,vy=at(1分)又因为粒子运动时间t=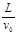 ,所以
,所以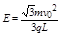 (1分)
(1分)
带电粒子在磁场中做圆周运动,洛伦兹力提供向心力,即: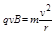 (1分)
(1分)
粒子离开电场时的速度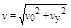 (1分)
(1分)
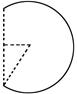
粒子在磁场中的运动轨迹如右图所示(1分)
由几何关系得,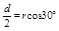 (1分)解得,
(1分)解得,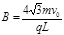 (1分)
(1分)
竖直方向:离开电场时的速度vy=v0tan30°(1分)粒子发生偏转的位移
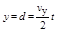 (1分)
(1分)水平方向:粒子匀速运动的时间
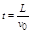 (1分)联立以上几式解得,
(1分)联立以上几式解得,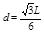 (1分)
(1分)(2)在电场中粒子受到电场力,由牛顿第二定律得,qE=ma(1分)
根据运动学公式有,vy=at(1分)又因为粒子运动时间t=
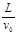 ,所以
,所以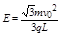 (1分)
(1分)带电粒子在磁场中做圆周运动,洛伦兹力提供向心力,即:
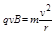 (1分)
(1分)粒子离开电场时的速度
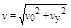 (1分)
(1分)
粒子在磁场中的运动轨迹如右图所示(1分)
由几何关系得,
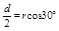 (1分)解得,
(1分)解得,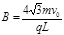 (1分)
(1分)
练习册系列答案
相关题目
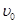 的速度垂直y轴射人第一象限内,经过电场后从x轴上x=2h的P2点以
的速度垂直y轴射人第一象限内,经过电场后从x轴上x=2h的P2点以 角射入x轴下方的匀强磁场.(重力不计)
角射入x轴下方的匀强磁场.(重力不计)
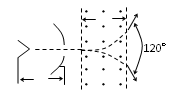


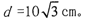
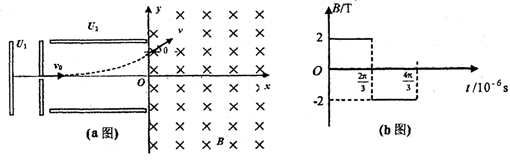
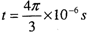 时粒子的位置坐标(X、Y)。(答案可以用根式表示,如用小数,请保留两位有效数字)
时粒子的位置坐标(X、Y)。(答案可以用根式表示,如用小数,请保留两位有效数字)