题目内容
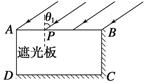
一玻璃立方体中心有一点状光源.今在立方体的部分表面镀上不透明薄膜,以致从光源发出的光线只经过一次折射不能透出立方体.已知该玻璃的折射率为,求镀膜的面积与立方体表面积之比的最小值
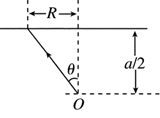


如图,考虑从玻璃立方体中心O点发出的一条光线,假设它斜射到玻璃立方体上表面发生折射.根据折射定律,有
 ①
①
式中,n是玻璃的折射率,入射角等于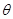 ,
, 是折射角.
是折射角.
现假设A点是上表面面积最小的不透明薄膜边缘上的一点.由题意,在A点刚好发生全反射,故
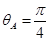 ②
②
设线段OA在立方体上表面的投影长为RA,由几何关系,有
 ③
③
由题意,上表面所镀的面积最小的不透明薄膜应是半径为RA的圆,所求的镀膜面积 与玻璃立方体的表面积S之比为
与玻璃立方体的表面积S之比为
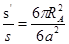 ④
④
 ①
①式中,n是玻璃的折射率,入射角等于
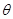 ,
, 是折射角.
是折射角.现假设A点是上表面面积最小的不透明薄膜边缘上的一点.由题意,在A点刚好发生全反射,故
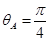 ②
②设线段OA在立方体上表面的投影长为RA,由几何关系,有
 ③
③由题意,上表面所镀的面积最小的不透明薄膜应是半径为RA的圆,所求的镀膜面积
 与玻璃立方体的表面积S之比为
与玻璃立方体的表面积S之比为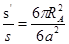 ④
④
练习册系列答案
相关题目

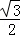 R.若该光束射入球体经一次反射后由E点(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c,则( )
R.若该光束射入球体经一次反射后由E点(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c,则( )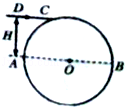
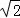
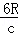
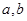 两束,它们与水面的夹角分别是
两束,它们与水面的夹角分别是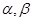 ,则
,则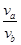 为( )
为( )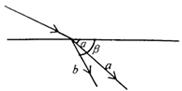
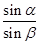
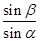
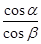
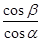
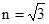 ,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆形玻璃砖的圆心O,结果在水平屏幕MN上出现两个光斑,则两个光斑之间的距离为
,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆形玻璃砖的圆心O,结果在水平屏幕MN上出现两个光斑,则两个光斑之间的距离为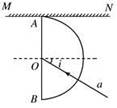
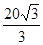 cm
cm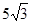 cm
cm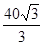 cm
cm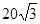 cm
cm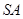 从水中射向空气后,折射出两束单色光
从水中射向空气后,折射出两束单色光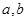 ,则下列判断正确的是( )
,则下列判断正确的是( )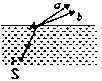
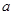 光的传播速度小于
光的传播速度小于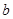 光的传播速度
光的传播速度 点顺时针方向转动,出射光线最先消失的是
点顺时针方向转动,出射光线最先消失的是