题目内容
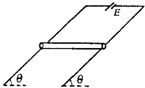
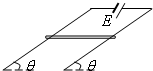
如图所示,两倾斜放置的光滑平行金属导轨间距为L,电阻不计,导轨平面与水平方向的夹角为θ,导轨上端接入一内电阻可忽略的电源,电动势为E.一粗细均匀的金属棒电阻为R,金属棒水平放在导轨上且与导轨接触良好.欲使金属棒静止于导轨上不动,则以下说法正确的是
A.可加竖直向下的匀强磁场,磁感应强度为B=mgRtanθ/EL
B.可加竖直向上的匀强磁场,磁感应强度为B=mgRtanθ/EL
C.所加匀强磁场磁感应强度的最小值为B=mgRsinθ/EL
D.如果金属棒的直径变为原来的二倍,原来静止的金属棒将沿导轨向下滑动
AC
解析:加竖直向下的匀强磁场时,棒受力如图a所示.

图a
由平衡条件得BIL=mgtanθ,
又因为I=![]() ,所以B=
,所以B=![]() ,故A正确.
,故A正确.
加竖直向上的匀强磁场时,棒受力如图b所示.

图b
金属棒在三个力作用下不可能处于平衡状态,故B错误.
要使棒在导轨上静止,磁感应强度最小,所加匀强磁场的方向必须垂直斜面斜向下,棒
受力如图c所示.由平衡条件知B![]() L=mgsinθ.
L=mgsinθ.

图c
所以B=mgRsinθ/EL,故C正确.
若金属棒的直径变为原来的两倍,则d=2d0.由S=![]() πd2得横截面积S=4S0.由R=ρ
πd2得横截面积S=4S0.由R=ρ![]() 得棒电阻R′=
得棒电阻R′=![]() R.
R.
由m=ρLS知棒质量m′=4m.若在图c受力情况下B![]() L=mgsinθ等式仍成立,故金属棒仍处于静止.故D错误.
L=mgsinθ等式仍成立,故金属棒仍处于静止.故D错误.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 如图所示,两倾斜放置的光滑平行金属导轨间距为L,电阻不计,导轨平面与水平方向的夹角为θ,导轨上端接入一内电阻可忽略的电源,电动势为E.一粗细均匀的金属棒电阻为R,金属棒水平放在导轨上且与导轨接触良好.欲使金属棒静止在导轨上不动,则以下说法正确的是( )
如图所示,两倾斜放置的光滑平行金属导轨间距为L,电阻不计,导轨平面与水平方向的夹角为θ,导轨上端接入一内电阻可忽略的电源,电动势为E.一粗细均匀的金属棒电阻为R,金属棒水平放在导轨上且与导轨接触良好.欲使金属棒静止在导轨上不动,则以下说法正确的是( )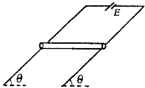 如图所示,两倾斜放置的光滑平行金属导轨间距为L,电阻不计,导轨平面与水平方向的夹角为θ.导轨上端接入一内电阻可忽略的电源,电动势为E.一粗细均匀的金属棒电阻为R.金属棒水平放在导轨上且与导轨接触良好,欲使金属棒静止于导轨上不动,则以下说法正确的是( )
如图所示,两倾斜放置的光滑平行金属导轨间距为L,电阻不计,导轨平面与水平方向的夹角为θ.导轨上端接入一内电阻可忽略的电源,电动势为E.一粗细均匀的金属棒电阻为R.金属棒水平放在导轨上且与导轨接触良好,欲使金属棒静止于导轨上不动,则以下说法正确的是( )