题目内容
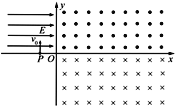
【题目】如图所示,固定在竖直平面内的光滑绝缘管道ABCDQ的A、Q两端与倾角θ=37°的传送带相切。不计管道内外径的差值.AB部分为半径R1=0.4 m的圆弧,CDQ部分也是圆弧。D为最高点,BC部分水平,且仅有BC段处于场强大小E=4×103 N/C,方向水平向右的匀强电场中,传送带长L=1.8 m,传送轮半径忽略不计。现将一可视为质点的带正电滑块从传送带上的Q处由静止释放,滑块能从A处平滑进入管道。已知滑块的质量m=l kg、电荷量q=5×10-4C.滑块与传送带之间的动摩擦因数μ=0.5,滑块通过管道与传送带的交接处时无速度损失,滑块电荷量始终保持不变,最大静摩擦力等于滑动摩擦力。g=10 m/s2。

(1)若传送带不动,求滑块第一次滑到A处的动能;
(2)若传送带不动,求滑块第一次滑到C处时所受圆弧轨道的弹力;
(3)改变传送带逆时针的转动速度以及滑块在Q处滑上传送带的初速度,可以使滑块刚滑上传送带就形成一个稳定的逆时针循环(即滑块每次通过装置中同一位置的速度相同)。在所有可能的循环中,求传送带速度的最小值。(结果可以用根号表示)
【答案】(1)3.6J(2)38.8N(3)![]()
【解析】试题分析:(1)滑块在传送带上滑动的过程中,有: ![]()
![]()
![]()
代入数据解得: ![]()
(2)由几何关系可得: ![]()
![]()
![]()
代入数据可得: ![]()
滑块由A到C的过程中,有![]()
滑块在圆弧C处,有![]()
联立以上各式并带入数据可解得滑块所受管道的弹力![]()
(3)要达到稳定的循环,要求每一循环中,对滑块需满足条件: ![]()
在滑块在传送带上时,速度大于传送带速度和小于传送带速度所对应的位移分别为![]() 和
和![]()
则![]()
![]()
代入数据可得: ![]()
所有可能的循环中,传送带速度最小所对应的情况是物体恰能够越过最高点D,即vD=0
此种情况下,物体从D点滑到与传送带等速的过程中
![]()
又![]()
联立以上各式解得: ![]()