题目内容
12. 如图所示是某一离子速度选择器原理示意图.在一半径为R=10cm 的圆柱形桶内有B=10-4T的匀强磁场,方向平行于轴线,在圆柱桶某一直径两端开有小孔,作为入射孔和出射孔,离x子束以不同角度入射,最后有不同速度的离子束射出,现有一离子源发射荷质比为2×1011C/kg的阳离子,且离子中速度分布连续,当角θ=45°,出射离子速度v的大小是( )
如图所示是某一离子速度选择器原理示意图.在一半径为R=10cm 的圆柱形桶内有B=10-4T的匀强磁场,方向平行于轴线,在圆柱桶某一直径两端开有小孔,作为入射孔和出射孔,离x子束以不同角度入射,最后有不同速度的离子束射出,现有一离子源发射荷质比为2×1011C/kg的阳离子,且离子中速度分布连续,当角θ=45°,出射离子速度v的大小是( )| A. | $\sqrt{2}$×106m/s | B. | 2$\sqrt{2}$×106m/s | C. | 2$\sqrt{2}$×108m/s | D. | $\sqrt{2}$×108m/s |
分析 离子束不经碰撞而直接从出身孔射出,即可根据几何知识画出轨迹,由几何关系求出轨迹的半径,即可由牛顿第二定律求速度v.
解答 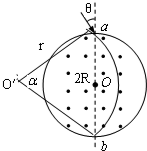 解:离子从小孔a射入磁场,与ab方向的夹角为θ=45°,则离子从小孔b离开磁场时速度与ab的夹角也为θ=45°,过入射速度和出射速度方向作垂线,得到轨迹的圆心O′,画出轨迹如图,由几何知识得到轨迹所对应的圆心角 α=2θ=90°,则由几何知识得:
解:离子从小孔a射入磁场,与ab方向的夹角为θ=45°,则离子从小孔b离开磁场时速度与ab的夹角也为θ=45°,过入射速度和出射速度方向作垂线,得到轨迹的圆心O′,画出轨迹如图,由几何知识得到轨迹所对应的圆心角 α=2θ=90°,则由几何知识得:
离子的轨迹半径为 r=$\sqrt{2}$R=10$\sqrt{2}$cm=0.1$\sqrt{2}$m
由牛顿第二定律得:
qvB=m$\frac{{v}^{2}}{r}$
得:v=$\frac{qBr}{m}$=2×1011×10-4×0.1$\sqrt{2}$=×10-4=2$\sqrt{2}$×106m/s
故选:B
点评 本题的解题关键是根据几何知识画出离子的运动轨迹,得到轨迹半径,即可求解速度v

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
2. 如图所示的天平可用来测定磁感应强度.天平的右臂下面挂有一个矩形线圈,宽度为l,共N匝,线圈下端悬在匀强磁场中,磁场方向垂直纸面.当线圈中通有电流I(方向如图)时,在天平左、右两边加上质量各为m1、m2的砝码,天平平衡,当电流反向(大小不变)时,右边再加上质量为m的砝码后,天平重新平衡,由此可知( )
如图所示的天平可用来测定磁感应强度.天平的右臂下面挂有一个矩形线圈,宽度为l,共N匝,线圈下端悬在匀强磁场中,磁场方向垂直纸面.当线圈中通有电流I(方向如图)时,在天平左、右两边加上质量各为m1、m2的砝码,天平平衡,当电流反向(大小不变)时,右边再加上质量为m的砝码后,天平重新平衡,由此可知( )
 如图所示的天平可用来测定磁感应强度.天平的右臂下面挂有一个矩形线圈,宽度为l,共N匝,线圈下端悬在匀强磁场中,磁场方向垂直纸面.当线圈中通有电流I(方向如图)时,在天平左、右两边加上质量各为m1、m2的砝码,天平平衡,当电流反向(大小不变)时,右边再加上质量为m的砝码后,天平重新平衡,由此可知( )
如图所示的天平可用来测定磁感应强度.天平的右臂下面挂有一个矩形线圈,宽度为l,共N匝,线圈下端悬在匀强磁场中,磁场方向垂直纸面.当线圈中通有电流I(方向如图)时,在天平左、右两边加上质量各为m1、m2的砝码,天平平衡,当电流反向(大小不变)时,右边再加上质量为m的砝码后,天平重新平衡,由此可知( )| A. | 磁感应强度的方向垂直纸面向里,大小为$\frac{({m}_{1}-{m}_{2})g}{NIl}$ | |
| B. | 磁感应强度的方向垂直纸面向里,大小为$\frac{mg}{2NIl}$ | |
| C. | 磁感应强度的方向垂直纸面向外,大小为$\frac{({m}_{1}-{m}_{2})g}{NIl}$ | |
| D. | 磁感应强度的方向垂直纸面向外,大小为$\frac{mg}{2NIl}$ |
7. 如图所示,在竖直平面内固定一个光滑绝缘的半圆形轨道,水平方向的匀强磁场与半圆形轨道所在的平面垂直,一个带负电荷的小滑块由静止开始从最高点M沿半圆轨道滑下,滑块始终未脱离圆轨道,则下列说法中正确的是( )
如图所示,在竖直平面内固定一个光滑绝缘的半圆形轨道,水平方向的匀强磁场与半圆形轨道所在的平面垂直,一个带负电荷的小滑块由静止开始从最高点M沿半圆轨道滑下,滑块始终未脱离圆轨道,则下列说法中正确的是( )
 如图所示,在竖直平面内固定一个光滑绝缘的半圆形轨道,水平方向的匀强磁场与半圆形轨道所在的平面垂直,一个带负电荷的小滑块由静止开始从最高点M沿半圆轨道滑下,滑块始终未脱离圆轨道,则下列说法中正确的是( )
如图所示,在竖直平面内固定一个光滑绝缘的半圆形轨道,水平方向的匀强磁场与半圆形轨道所在的平面垂直,一个带负电荷的小滑块由静止开始从最高点M沿半圆轨道滑下,滑块始终未脱离圆轨道,则下列说法中正确的是( )| A. | 滑块经过最低点时的速度比磁场不存在时大 | |
| B. | 滑块经过最低点时的速度大小与磁场不存在时相等 | |
| C. | 滑块从M点第一次滑到最低点对轨道的压力比磁场不存在时小 | |
| D. | 滑块从M点滑到最低点与再次返回最低点对轨道的压力大小相同 |
1.在匀变速直线运动中,下面关于速度和加速度关系的说法,正确的是( )
| A. | 加速度变大,速度一定变大 | B. | 加速度减小时,速度一定减小 | ||
| C. | 速度为零,加速度也一定为零 | D. | 速度增大时,加速度也可能减小 |
2.一质量为m的滑块从倾斜角为a的,足够长的光滑斜面上由静止开始释放并开始计时,t时刻重力对它做功的瞬时功率为( )
| A. | mg2t | B. | mg2tsina | C. | mg2tsin2a | D. | $\frac{1}{2}$mg2tsin2a |
 一辆汽车在平直的路面上行驶,其位移-时间图象(s-t图象)如图所示.根据图象可知,该汽车做匀速(填“匀速”或“匀加速”)直线运动;在0~20s内汽车的位移大s=400m.
一辆汽车在平直的路面上行驶,其位移-时间图象(s-t图象)如图所示.根据图象可知,该汽车做匀速(填“匀速”或“匀加速”)直线运动;在0~20s内汽车的位移大s=400m.
 现要验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.给定的器材如下:一倾角可以调节的长斜面(如图)、小车、计时器一个、米尺.
现要验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.给定的器材如下:一倾角可以调节的长斜面(如图)、小车、计时器一个、米尺.