题目内容
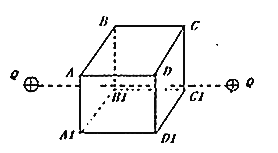
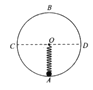
【题目】如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点, 已知弹簧的劲度系数为k=mg/R,原长为L=2R,弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )
A.无论v0多大,小球均不会离开圆轨道
B.若在![]() 则小球会在B.D间脱离圆轨道
则小球会在B.D间脱离圆轨道
C.只要![]() ,小球就能做完整的圆周运动.
,小球就能做完整的圆周运动.
D.只要小球能做完整圆周运动,则小球与轨道间最大压力与最小压力之差恒为6mg
【答案】ACD
【解析】
AB.弹簧的劲度系数为![]() ,原长为L=2R,所以小球始终会受到弹簧的弹力作用,大小为F=k(L-R)=kR=mg,方向始终背离圆心,无论小球在CD以上的哪个位置速度为零,重力在沿半径方向上的分量都小于等于弹簧的弹力(在CD以下,轨道对小球一定有指向圆心的支持力),所以无论v0多大,小球均不会离开圆轨道。故A符合题意,B不符合题意。
,原长为L=2R,所以小球始终会受到弹簧的弹力作用,大小为F=k(L-R)=kR=mg,方向始终背离圆心,无论小球在CD以上的哪个位置速度为零,重力在沿半径方向上的分量都小于等于弹簧的弹力(在CD以下,轨道对小球一定有指向圆心的支持力),所以无论v0多大,小球均不会离开圆轨道。故A符合题意,B不符合题意。
C.小球在运动过程中只有重力做功,弹簧的弹力和轨道的支持力不做功,机械能守恒,当运动到最高点速度为零,在最低点的速度最小,有![]() ,解得:
,解得:
![]()
所以只要![]() ,小球就能做完整的圆周运动,故C符合题意。
,小球就能做完整的圆周运动,故C符合题意。
D.在最低点时,设小球受到的支持力为N,根据牛顿第二定律有:![]() ,解得:
,解得:
![]()
运动到最高点时受到轨道的支持力最小,设为N′,设此时的速度为v,由机械能守恒有:![]() ,此时合外力提供向心力,有:
,此时合外力提供向心力,有:![]() ,可得:
,可得:![]() 。联立可得压力差为:△N=6mg,与初速度无关。故D符合题意。
。联立可得压力差为:△N=6mg,与初速度无关。故D符合题意。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目