题目内容
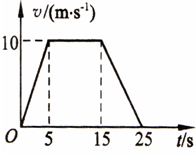
 在升降机中的水平底板上放一质量为60kg的物体,如图所示为升降机下降过程中的υ-t图象,试通过计算回答.(g取10m/s2)
在升降机中的水平底板上放一质量为60kg的物体,如图所示为升降机下降过程中的υ-t图象,试通过计算回答.(g取10m/s2)物体在0-5s、5-15s、15-25s内运动的加速度为多大?物体对升降机底板的压力各是多大?
分析:根据图线的斜率求出加速度,通过牛顿第二定律求出支持力的大小,从而求出物体对升降机底板的压力大小.
解答:解:运动过程分三个阶段:
第一阶段,初速度为零的向下匀加速运动,由图象得a1=
m/s2=2m/s2
由牛顿第二定律得mg-F1=ma1F1=m(g-a1)=60×(10-2)N=480N
第二阶段,匀速向下运动,物体处于平衡状态,加速度为零,由牛顿第二定律得mg-F2=0,
即 F2=mg=600N
第三阶段,向下匀减速运动,由15~25s间的速度图象可知a3=
m/s2=-1m/s2
由牛顿第二定律得mg-F3=ma3,F3=m(g-a3)=60×[10-(-1)]N=660N
答:物体在0-5s、5-15s、15-25s内运动的加速度分别为2m/s2,0,-1m/s2.物体对升降机底板的压力各是480N,600N,660N.
第一阶段,初速度为零的向下匀加速运动,由图象得a1=
| 10 |
| 5 |
由牛顿第二定律得mg-F1=ma1F1=m(g-a1)=60×(10-2)N=480N
第二阶段,匀速向下运动,物体处于平衡状态,加速度为零,由牛顿第二定律得mg-F2=0,
即 F2=mg=600N
第三阶段,向下匀减速运动,由15~25s间的速度图象可知a3=
| -10 |
| 10 |
由牛顿第二定律得mg-F3=ma3,F3=m(g-a3)=60×[10-(-1)]N=660N
答:物体在0-5s、5-15s、15-25s内运动的加速度分别为2m/s2,0,-1m/s2.物体对升降机底板的压力各是480N,600N,660N.
点评:解决本题的关键知道速度时间图线的斜率表示加速度,通过加速度的方向,结合牛顿第二定律进行求解.

练习册系列答案
相关题目

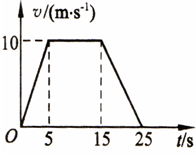 在升降机中的水平底板上放一质量为60kg的物体,如图所示为升降机下降过程中的υ-t图象,试通过计算回答.(g取10m/s2)
在升降机中的水平底板上放一质量为60kg的物体,如图所示为升降机下降过程中的υ-t图象,试通过计算回答.(g取10m/s2)