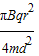题目内容
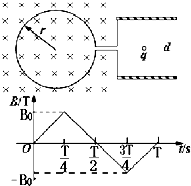
半径为r带极小缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定水平放置的平行金属板连接,两板间距为d.有一变化的磁场垂直于纸面,规定向内为正,变化规律如图所示.在t=0时刻平板之间中心有一重力不计,电荷量为q、质量为m的静止微粒,微粒带正电.如果前T秒内粒子未碰到平行金属板,则以下说法正确的是( )
A.
| ||||
B.
| ||||
C.
| ||||
D.第2T秒末微粒离出发点最远,距离为
|

A、在前
秒内,磁场随着时间均匀增加,则由法拉第电磁感应定律得,感应电动势是恒定不变的,再由楞次定律可得金属板上极带负电.所以带电粒子在电场力作用下向上运动.当后
秒内,磁场随着时间均匀减小,则由法拉第电磁感应定律得,感应电动势是恒定不变的,再由楞次定律可得金属板上极带正电.故A正确;
B、在
秒到
秒内,磁场随着时间均匀增加,不过方向是垂直纸面向外,则由法拉第电磁感应定律得,感应电动势是恒定不变的,再由楞次定律可得金属板上极带正电,则带电粒子反向做匀加速,加速度大小为
=
所以速度大小v=at=
×
=
,方向竖直向下.故B正确;
C、在前
秒内,磁场随着时间均匀增加,则由法拉第电磁感应定律得,感应电动势是恒定不变的,再由楞次定律可得金属板上极带负电.所以带电粒子在电场力作用下向上运动.当后
秒内,磁场随着时间均匀减小,则由法拉第电磁感应定律得,感应电动势是恒定不变的,再由楞次定律可得金属板上极带正电.所以带电粒子向上先做匀加速后做匀减速.故C错误;
D、在前
秒内,磁场随着时间均匀增加,则由法拉第电磁感应定律得,感应电动势是恒定不变的,再由楞次定律可得金属板上极带负电.所以带电粒子在电场力作用下向上运动.当后
秒内,磁场随着时间均匀减小,则由法拉第电磁感应定律得,感应电动势是恒定不变的,再由楞次定律可得金属板上极带正电.所以带电粒子向上先做匀加速后做匀减速.由此可得,在第T秒内,粒子回到原点,则第2T秒内,粒子仍然回到原点.故D错误;
故选:AB
| T |
| 4 |
| T |
| 4 |
B、在
| T |
| 2 |
| 3T |
| 4 |
| qE |
| m |
| 4qB0πr2 |
| mTd |
所以速度大小v=at=
| 4qB0πr2 |
| mTd |
| T |
| 4 |
| πB0qr2 |
| md |
C、在前
| T |
| 4 |
| T |
| 4 |
D、在前
| T |
| 4 |
| T |
| 4 |
故选:AB

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 半径为r带极小缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定水平放置的平行金属板连接,两板间距为d.有一变化的磁场垂直于纸面,规定向内为正,变化规律如图所示.在t=0时刻平板之间中心有一重力不计,电荷量为q、质量为m的静止微粒,微粒带正电.如果前T秒内粒子未碰到平行金属板,则以下说法正确的是( )
半径为r带极小缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定水平放置的平行金属板连接,两板间距为d.有一变化的磁场垂直于纸面,规定向内为正,变化规律如图所示.在t=0时刻平板之间中心有一重力不计,电荷量为q、质量为m的静止微粒,微粒带正电.如果前T秒内粒子未碰到平行金属板,则以下说法正确的是( )
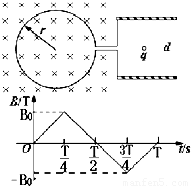
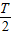 秒时平行金属板上极板为正极
秒时平行金属板上极板为正极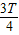 秒时速度大小为
秒时速度大小为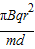 ,方向竖直向下
,方向竖直向下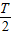 秒时微粒回到了原来位置
秒时微粒回到了原来位置