题目内容
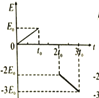
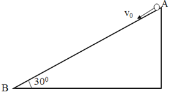
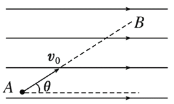
【题目】真空中某竖直平面内存在一水平向右的匀强电场，一质量为m的带电小球恰好能沿图示虚线(与水平方向成θ角)由A向B做直线运动，小球的初速度为v0，重力加速度为g，则
A.小球可以带正电
B.小球向上运动过程中动能和重力势能之和在减小
C.可求出小球运动到最高点所用的时间
D.不能求出小球运动到最高点电势能的改变量
【答案】BC
【解析】
A．小球做直线运动的条件是速度方向和合外力的方向在同一条直线上，小球受到竖直向下的重力，只有小球受到水平向左的电场力才能使得合力方向与速度方向相反且在同一条直线上，由此可知小球所受的电场力的方向与场强方向相反，则小球必带负电，故A错误；
B．小球向上运动过程中只有重力和电场力做功，则小球的动能、重力势能和电势能之和守恒，因从A到B电场力做负功，电势能增加，则动能和重力势能之和在减小，选项B正确；
C．小球的加速度满足：
且由
可求解小球运动到最高点所用的时间，选项C正确；
D．由选项B的分析可知，可求得到达最高点时机械能的减小量为
其中
则可求出小球运动到最高点电势能的增加量也为E，选项D错误；
故选BC.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
