题目内容
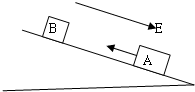 (2004?广州二模)在倾角为θ的足够长的绝缘斜面上,带负电的物块A和不带电的绝缘物块B正沿斜面往上滑,斜面处于范围足够大的匀强电场中,场强方向平行斜面向下.当A刚要追上B时,A的速度vA=1.8m/s,方向沿斜面向上,B的速度恰为零,如图所示,A、B碰撞过程相互作用时间极短、且A的电荷没有转移,碰后瞬间A的速度v1=0.6m/s,方向仍沿斜面向上.碰后经0.60s,A的速率变为v2=1.8m/s,在这段时间内两者没有再次相碰.已知A和斜面间的动摩擦因数μ=0.15,B与斜面的摩擦忽略不计,A、B均可视为质点,它们质量分别为mA=0.5kg、mB=0.25kg,匀强电场的场强E=5×106N/C,sin θ=0.6,g=10m/s2.
(2004?广州二模)在倾角为θ的足够长的绝缘斜面上,带负电的物块A和不带电的绝缘物块B正沿斜面往上滑,斜面处于范围足够大的匀强电场中,场强方向平行斜面向下.当A刚要追上B时,A的速度vA=1.8m/s,方向沿斜面向上,B的速度恰为零,如图所示,A、B碰撞过程相互作用时间极短、且A的电荷没有转移,碰后瞬间A的速度v1=0.6m/s,方向仍沿斜面向上.碰后经0.60s,A的速率变为v2=1.8m/s,在这段时间内两者没有再次相碰.已知A和斜面间的动摩擦因数μ=0.15,B与斜面的摩擦忽略不计,A、B均可视为质点,它们质量分别为mA=0.5kg、mB=0.25kg,匀强电场的场强E=5×106N/C,sin θ=0.6,g=10m/s2.(1)A、B第一次碰撞后瞬间,B的速度多大?
(2)第一次碰后的0.60s内B沿斜面向上最多滑多远?
(3)分析第一次碰撞后至0.60s这段时间内A的运动方向并求出A的电量.
分析:(1)由于A、B碰撞过程相互作用时间极短,合外力的冲量近似为零,系统的动量认为守恒,根据动量守恒定律求解A、B第一次碰撞后瞬间B的速度;
(2)根据牛顿第二定律和运动学公式结合求解第一次碰后的0.60s内B沿斜面向上滑行的最大距离;
(3)碰后的0.60s内,A的运动有两种可能:一直加速向上,或减速向上再加速向下.
设A的加速度为aA.第一情况下,两个物体能发生第二次碰撞,根据运动学公式求出A的加速度aA.当两者位移相等时,第二次碰撞,求出时间,与0.60s比较,判断第一种情况是否可能发生.
对于第二种情况,分上滑和下滑两个过程进行研究,先由运动学公式求出加速度,再根据牛顿第二定律列式,即可求得A的电量.
(2)根据牛顿第二定律和运动学公式结合求解第一次碰后的0.60s内B沿斜面向上滑行的最大距离;
(3)碰后的0.60s内,A的运动有两种可能:一直加速向上,或减速向上再加速向下.
设A的加速度为aA.第一情况下,两个物体能发生第二次碰撞,根据运动学公式求出A的加速度aA.当两者位移相等时,第二次碰撞,求出时间,与0.60s比较,判断第一种情况是否可能发生.
对于第二种情况,分上滑和下滑两个过程进行研究,先由运动学公式求出加速度,再根据牛顿第二定律列式,即可求得A的电量.
解答:解:A、B碰撞时间极短,沿斜面的方向动量守恒,设碰后瞬间B的速度为vB
mAvA=mv1+mBvB
代入数字得:vB=2.4m/s
(2)B的加速度aB=-gsin θ=-6m/s2
B沿斜面上滑的最远距离SB=
=
m=0.48m
(3)碰后的0.60s内,A的运动有两种可能:一直加速向上,或减速向上再加速向下.设A的加速度为aA.
第一种情况:以沿斜面向上的方向为正方向,A向上的加速度aA=
=2m/s2 ①
第二次相遇的条件是两物位移相等:SA1=SB1,
即 v1t′+
aAt′2=vBt′+
aBt′2 ②
代入数字解出 t'=0.45s<0.60s,显然假设不符合题意.③
所以A的运动只能是第二种情况.设A向上运动时间为△t、加速度为a1,向下运动时加速度为a2,A受到的电场力为F,以沿斜面向上的方向为正方向,t=0.60s
a1=
④
a2=
⑤
分别对上滑和下滑过程运用牛顿第二定律列方程
上滑过程:F-mAgsin θ-μmAgcos θ=mAa1 ⑥
下滑过程:F-mAgsin θ+μmAgcos θ=mAa2 ⑦
联立方程④至⑦得:F=0.6N
根据F=EqA带电量 q=
=1.2×10-7C
答:
(1)A、B第一次碰撞后瞬间,B的速度为=2.4m/s.
(2)第一次碰后的0.60s内B沿斜面向上最多滑S0.48m.
(3)第一次碰撞后至0.60s这段时间内A受到的电场力为F,以沿斜面向上的方向为正方向,A的电量为1.2×10-7C.
mAvA=mv1+mBvB
代入数字得:vB=2.4m/s
(2)B的加速度aB=-gsin θ=-6m/s2
B沿斜面上滑的最远距离SB=
| ||
| 2aB |
| 0-2.42 |
| 2×(-6) |
(3)碰后的0.60s内,A的运动有两种可能:一直加速向上,或减速向上再加速向下.设A的加速度为aA.
第一种情况:以沿斜面向上的方向为正方向,A向上的加速度aA=
| v2-v1 |
| t |
第二次相遇的条件是两物位移相等:SA1=SB1,
即 v1t′+
| 1 |
| 2 |
| 1 |
| 2 |
代入数字解出 t'=0.45s<0.60s,显然假设不符合题意.③
所以A的运动只能是第二种情况.设A向上运动时间为△t、加速度为a1,向下运动时加速度为a2,A受到的电场力为F,以沿斜面向上的方向为正方向,t=0.60s
a1=
| 0-v1 |
| t |
a2=
| -v2 |
| t-△t |
分别对上滑和下滑过程运用牛顿第二定律列方程
上滑过程:F-mAgsin θ-μmAgcos θ=mAa1 ⑥
下滑过程:F-mAgsin θ+μmAgcos θ=mAa2 ⑦
联立方程④至⑦得:F=0.6N
根据F=EqA带电量 q=
| F |
| E |
答:
(1)A、B第一次碰撞后瞬间,B的速度为=2.4m/s.
(2)第一次碰后的0.60s内B沿斜面向上最多滑S0.48m.
(3)第一次碰撞后至0.60s这段时间内A受到的电场力为F,以沿斜面向上的方向为正方向,A的电量为1.2×10-7C.
点评:本题的过程比较复杂,按时间顺序进行分析.关键要分析第一次碰后A可能的运动情况,运用牛顿第二定律和运动学公式结合进行求解.

练习册系列答案
相关题目
 (2004?广州二模)“二分频”音箱内有两个不同口径的扬声器,它们的固有频率分别处于高音、低音频段,分别称为高音扬声器和低音扬声器,音箱要将扩音机送来的含有不同频率的混合音频电流按高、低频段分离出来,送往相应的扬声器,以便使电流所携带的音频信息按原比例还原成高、低频的机械振动图为音箱的电路图,高、低频混合电流由a、b输入,L1和L2是线圈,C1和C2是电容器( )
(2004?广州二模)“二分频”音箱内有两个不同口径的扬声器,它们的固有频率分别处于高音、低音频段,分别称为高音扬声器和低音扬声器,音箱要将扩音机送来的含有不同频率的混合音频电流按高、低频段分离出来,送往相应的扬声器,以便使电流所携带的音频信息按原比例还原成高、低频的机械振动图为音箱的电路图,高、低频混合电流由a、b输入,L1和L2是线圈,C1和C2是电容器( ) (2004?广州二模)如图所示,绝缘光滑的半圆轨道位于竖直平面内,并处于竖直向下的匀强电场中,在轨道的上缘有一个质量为m,带电荷量为+q的小球,由静止开始沿轨道运动.下列说法正确的是( )
(2004?广州二模)如图所示,绝缘光滑的半圆轨道位于竖直平面内,并处于竖直向下的匀强电场中,在轨道的上缘有一个质量为m,带电荷量为+q的小球,由静止开始沿轨道运动.下列说法正确的是( )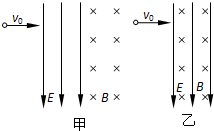 (2004?广州二模)一重力不计的带电粒子一初速度v0先后穿过宽度相同且紧邻在一起的有明显边界的匀强电场E和匀强磁场B,如图甲所示,电场和磁场对粒子总共做功W1;若把电场和磁场正交叠加,如图乙所示,粒子仍以v0的初速度穿过叠加场区对粒子总共做功W2,比较W1、W2的绝对值大小( )
(2004?广州二模)一重力不计的带电粒子一初速度v0先后穿过宽度相同且紧邻在一起的有明显边界的匀强电场E和匀强磁场B,如图甲所示,电场和磁场对粒子总共做功W1;若把电场和磁场正交叠加,如图乙所示,粒子仍以v0的初速度穿过叠加场区对粒子总共做功W2,比较W1、W2的绝对值大小( )