题目内容
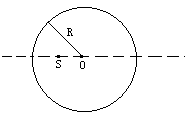如图所示为一个透明介质制成的半径为R的球，透明介质的折射率为n，球心为O．透明球内有一点光源S，S距球心O的距离为R/n．试证明：光源S发出的光射到右边球面上，经球面折射后能形成像
，并求出像的位置．
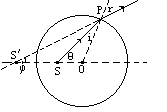如图所示，设入射角为i入射光与主轴的夹角为θ，折射角为r。在三角形PSO中，由三角形关系可知：
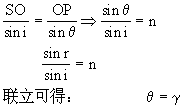
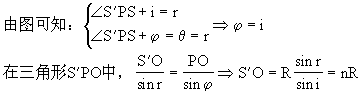
解析:
如图所示，设入射角为i入射光与主轴的夹角为θ，折射角为r。在三角形PSO中，由三角形关系可知：
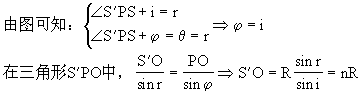
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
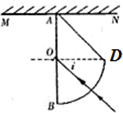如图所示为某种透明介质的截面图，△AOD为等腰直角三角形，BD为半径R=10cm的四分之一圆弧，AB与水平屏幕MN垂直并接触于A点．一束细紫色光沿圆弧的半径方向射向圆心O，在AB分界面上的入射角i=45°．已知该介质对紫光的折射率为n=| 2 |
| A、紫光射到AB面后，可能有折射光从AB面射出，也可能没有折射光射出 | ||||
| B、紫光在屏幕上只形成一个光点，该光点与A点相距10cm | ||||
C、若射向O点的是由该紫光和折射率为
| ||||
| D、若能观察到红光穿过某小孔的衍射现象，则能更明显观察到紫光穿过该小孔的衍射现象 |
，并求出像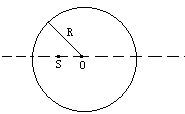
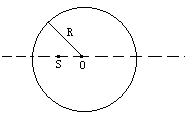如图所示为一个透明介质制成的半径为R的球，透明介质的折射率为n，球心为O．透明球内有一点光源S，S距球心O的距离为R/n．试证明：光源S发出的光射到右边球面上，经球面折射后能形成像
，并求出像
。则
的红光组成的复色光，屏幕上形成三个光点