题目内容
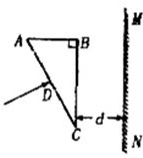 (2013?泰安一模)如图所示,一截面是直角三角形的棱镜ABC,∠C=30°.在距BC边d处有一与BC边平行的光屏MN.现有某一单色光束从AC边的中点D垂直AC边射入棱镜.已知棱镜对该单色光束折射率为n=
(2013?泰安一模)如图所示,一截面是直角三角形的棱镜ABC,∠C=30°.在距BC边d处有一与BC边平行的光屏MN.现有某一单色光束从AC边的中点D垂直AC边射入棱镜.已知棱镜对该单色光束折射率为n=| 3 |
分析:根据几何关系求出在BC边上的入射角,通过折射定律求出在BC边上的折射角,根据几何关系求出从BC边第一次到达MN的距离,通过光速求出BC边第一次出射到达MN的时间.
解答:解:光从BC边射出时出射角为θ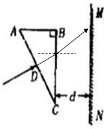
n=
θ=60°
由几何关系知,光从BC边射出到达屏MN的路程为2d
光从BC到达MN经历的时间t=
.
答:该光束从BC边第一次出射到达MN的时间为
.

n=
| sinθ |
| sin30° |
θ=60°
由几何关系知,光从BC边射出到达屏MN的路程为2d
光从BC到达MN经历的时间t=
| 2d |
| c |
答:该光束从BC边第一次出射到达MN的时间为
| 2d |
| c |
点评:本题考查几何光学问题,关键掌握光的折射定律n=
.
| sinθ |
| sinα |

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
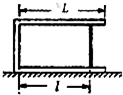 (2013?泰安一模)气缸长为L=1m,固定在水平面上,气缸中有横截面积为S=100cm2的光滑活塞,活塞封闭了一定质量的理想气体,当温度为t=27℃,大气压强为P0=1×105Pa时,气柱长度为l=90cm,气缸和活塞的厚度均可忽略不计.求:
(2013?泰安一模)气缸长为L=1m,固定在水平面上,气缸中有横截面积为S=100cm2的光滑活塞,活塞封闭了一定质量的理想气体,当温度为t=27℃,大气压强为P0=1×105Pa时,气柱长度为l=90cm,气缸和活塞的厚度均可忽略不计.求: (2013?泰安一模)如图所示为一列沿x轴正向传播的简谐横波在t=0时刻的图象,振源周期为1s.以下说法正确的是( )
(2013?泰安一模)如图所示为一列沿x轴正向传播的简谐横波在t=0时刻的图象,振源周期为1s.以下说法正确的是( )