题目内容
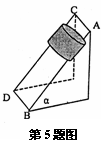
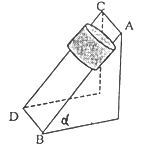
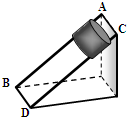 如图所示,两根直棒AB和CD相互平行,斜靠在竖直墙壁上固定不动,一圆筒从棒的上端沿棒匀速滑下.若要使圆筒加速下滑,以下措施可行的是
如图所示,两根直棒AB和CD相互平行,斜靠在竖直墙壁上固定不动,一圆筒从棒的上端沿棒匀速滑下.若要使圆筒加速下滑,以下措施可行的是
- A.增大两棒间的距离
- B.减小两棒间的距离
- C.增大两棒的倾角
- D.减小圆筒的质量
BC
分析:1、圆筒受重力、滑动摩擦力(两个)、支持力(两个),匀速直线运动时受力平衡;将两棍间的距离减小后固定不动,支持力(两个)的合力仍然等于重力的垂直分力,夹角减小,故两个支持力变小,故滑动摩擦力变小,根据牛顿第二定律列式得到加速度的变化情况.
2、两棒间的距离不变,滑动摩擦力,摩擦力等于mgcosθ,根据牛顿第二定律:mgsinθ-μmgcosθ=ma,即a=gsinθ-μgcosθ,θ变化,加速度就会变化,但是与物体质量无关.
解答:A、B:圆筒从棒的上端匀速滑下过程中,受到重力、两棒的支持力和摩擦力,根据平衡条件得知:mgsinθ-2f1=0
将两棒间的距离稍减小后,两棒支持力的合力不变,夹角减小,每根木棒对圆筒的支持力减小,滑动摩擦力减小,根据牛顿第二定律,有:mgsinθ-2f2=ma,由于摩擦力变小,故加速度变大,可知圆筒将匀加速滑动.故A错误、B正确.
C、增大两棒的倾角,两棒支持力的合力仍等于重力垂直于棒子向上的分力,但是由于倾角变大,故重力垂直于棒子向上的分力变小,即摩擦力变小,而重力沿着棒子向下的分力变大,根据牛顿第二定律:mgsinθ-μmgcosθ=ma,即a=gsinθ-μgcosθ,所以a变大,物体加速运动.故C正确.
D、根据牛顿第二定律:mgsinθ-μmgcosθ=ma,即a=gsinθ-μgcosθ,可知加速度与圆筒的质量无关.故D错误.
故选BC.
点评:本题中运用到推论:当两个分力大小一定时,夹角增大时,其合力减小,分析两棍支持力的变化.
分析:1、圆筒受重力、滑动摩擦力(两个)、支持力(两个),匀速直线运动时受力平衡;将两棍间的距离减小后固定不动,支持力(两个)的合力仍然等于重力的垂直分力,夹角减小,故两个支持力变小,故滑动摩擦力变小,根据牛顿第二定律列式得到加速度的变化情况.
2、两棒间的距离不变,滑动摩擦力,摩擦力等于mgcosθ,根据牛顿第二定律:mgsinθ-μmgcosθ=ma,即a=gsinθ-μgcosθ,θ变化,加速度就会变化,但是与物体质量无关.
解答:A、B:圆筒从棒的上端匀速滑下过程中,受到重力、两棒的支持力和摩擦力,根据平衡条件得知:mgsinθ-2f1=0
将两棒间的距离稍减小后,两棒支持力的合力不变,夹角减小,每根木棒对圆筒的支持力减小,滑动摩擦力减小,根据牛顿第二定律,有:mgsinθ-2f2=ma,由于摩擦力变小,故加速度变大,可知圆筒将匀加速滑动.故A错误、B正确.
C、增大两棒的倾角,两棒支持力的合力仍等于重力垂直于棒子向上的分力,但是由于倾角变大,故重力垂直于棒子向上的分力变小,即摩擦力变小,而重力沿着棒子向下的分力变大,根据牛顿第二定律:mgsinθ-μmgcosθ=ma,即a=gsinθ-μgcosθ,所以a变大,物体加速运动.故C正确.
D、根据牛顿第二定律:mgsinθ-μmgcosθ=ma,即a=gsinθ-μgcosθ,可知加速度与圆筒的质量无关.故D错误.
故选BC.
点评:本题中运用到推论:当两个分力大小一定时,夹角增大时,其合力减小,分析两棍支持力的变化.

练习册系列答案
相关题目
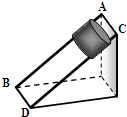 如图所示,两根直棒AB和CD相互平行,斜靠在竖直墙壁上固定不动,一圆筒从棒的上端沿棒匀速滑下.若要使圆筒加速下滑,以下措施可行的是( )
如图所示,两根直棒AB和CD相互平行,斜靠在竖直墙壁上固定不动,一圆筒从棒的上端沿棒匀速滑下.若要使圆筒加速下滑,以下措施可行的是( )| A、增大两棒间的距离 | B、减小两棒间的距离 | C、增大两棒的倾角 | D、减小圆筒的质量 |
 如图所示,两根直棒AB和CD相互平行,斜靠在竖直墙壁上固定不动,一圆筒从棒的上端沿棒匀速滑下;若要使圆筒加速下滑,以下措施可行的是( )
如图所示,两根直棒AB和CD相互平行,斜靠在竖直墙壁上固定不动,一圆筒从棒的上端沿棒匀速滑下;若要使圆筒加速下滑,以下措施可行的是( )| A、保持两棒的倾角不变,减小两棒间的距离 | B、保持两棒的倾角不变,增加两棒间的距离 | C、保持两棒间的距离不变,减小两棒的倾角 | D、增加圆筒的质量 |