题目内容
一物体在外力的作用下从静止开始做直线运动，合外力的方向不变，大小随时间的变化如图所示．设该物体在t0和2t0时刻相对于出发点的位移分别为x1和x2，速度分别为v1和v2；合外力在0-t0和t0-2t0时间内做的功分别为W1和W2，则（ ）分析：由牛顿第二定律可以求得物体在两段时间的加速度的大小，在由位移的公式可以分别求得速度、位移的关系，根据动能定理可以求得合力做功的关系．
解答：解：由于物体受的合力是2倍的关系，根据牛顿第二定律F=ma可知，加速度也是2倍的关系，即a2=2a1，
所以物体的位移 x1=
a1t02，速度为 v1=a1t0，做的功为 W1=F0?x1，
物体的位移为 x2=x1+V1t0+
a2t02=a1t0?t0+
2a1t02=
a1t02，得x1：x2=1：5，
速度为 v2=v1+a2t0=3v1，得v1：v2=1：3
做的功为 W2=2F0?（x2-x1）=8W1．得W1：W2=1：8
所以C正确．
故选C．
所以物体的位移 x1=
| 1 |
| 2 |
物体的位移为 x2=x1+V1t0+
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
速度为 v2=v1+a2t0=3v1，得v1：v2=1：3
做的功为 W2=2F0?（x2-x1）=8W1．得W1：W2=1：8
所以C正确．
故选C．
点评：本题在计算时要注意，位移x1和x2都是相对于出发点的位移，并不是各自时间内经过的位移．
练习册系列答案
导学全程练创优训练系列答案
相关题目
（2009?海南）一物体在外力的作用下从静止开始做直线运动，合外力方向不变，大小随时间的变化如图所示．设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2，速度分别是v1和v2，合外力从开始至t0时刻做的功是W1，从t0至2t0时刻做的功是W2，则（ ）
（2011?普陀区二模）一物体在外力的作用下从静止开始做直线运动，合外力的方向不变，大小随时间的变化如图所示．设该物体在t0和2t0时刻相对于出发点的位移分别为x1和x2，速度分别为v1和v2；合外力在0-t0和t0-2t0时间内做的功分别为W1和W2，在t0和2t0时刻的功率分别为P1和P2，则（ ）
（2009?上海模拟）一物体在外力的作用下从静止开始做直线运动，合外力方向不变，大小随时间的变化如图所示．设该物体在to和2to时刻的速度大小分别为v1和v2，合外力从开始至to时刻做的功是w1，从to至2to时刻做的功是w2，则v2=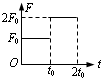
一物体在外力的作用下从静止开始做直线运动，合外力方向不变，大小随时间的变化如图所示．设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2，则x1和x2的关系是