题目内容
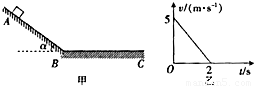
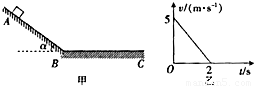
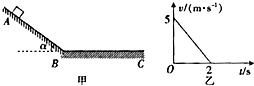如图甲所示，斜面AB和水平面BC与滑块间的动摩擦因数相同，AB斜面的倾角α=37°．一质进为1kg的滑块从AU斜面上由静止开始下滑，不计滑块经过连接处B的能量损失，从 滑块滑上水平面BC开始计时，其运动的图象如图乙所示．重力加速度g取10m/s2，已知sin37°=0.6，cos37°=0.8．试求：
（1）滑块与水平面间的动摩擦因数．
（2）滑块开始下滑处到B点的距离．
解：（1）由题中乙图可知，滑块在水平面上的初速度v=5m/s，运动t=2s后停止，则滑块的加速度大小：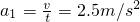
．
根据牛顿第二定律有：μmg=ma1
解得：μ=0.25．
（2）滑块在AB斜面上运动时有：mgsinθ-μmgcosθ=ma2
解得：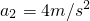
．
由运动学公式：v2=2a2x得：x=3.125m．
答：（1）滑块与水平面间的动摩擦因数为0.25．
（2）滑块开始下滑处到B点的距离为3.125m．
分析：（1）从图象可知，物块在水平面做匀减速直线运动，根据图线求出匀减速直线运动的加速度大小，结合牛顿第二定律求出滑块与水平面间的动摩擦因数．
（2）根据牛顿第二定律求出物块在斜面上的加速度，结合末速度，运用速度位移公式求出滑块开始下滑处到B点的距离．
点评：解决本题的关键知道加速度是联系力学和运动学的桥梁，通过加速度可以根据力求运动，也可以根据运动求力．
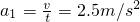．根据牛顿第二定律有：μmg=ma1
解得：μ=0.25．
（2）滑块在AB斜面上运动时有：mgsinθ-μmgcosθ=ma2
解得：
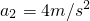．由运动学公式：v2=2a2x得：x=3.125m．
答：（1）滑块与水平面间的动摩擦因数为0.25．
（2）滑块开始下滑处到B点的距离为3.125m．
分析：（1）从图象可知，物块在水平面做匀减速直线运动，根据图线求出匀减速直线运动的加速度大小，结合牛顿第二定律求出滑块与水平面间的动摩擦因数．
（2）根据牛顿第二定律求出物块在斜面上的加速度，结合末速度，运用速度位移公式求出滑块开始下滑处到B点的距离．
点评：解决本题的关键知道加速度是联系力学和运动学的桥梁，通过加速度可以根据力求运动，也可以根据运动求力．
练习册系列答案
相关题目
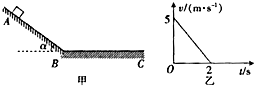如图甲所示，斜面AB和水平面BC与滑块间的动摩擦因数相同，AB斜面的倾角α=37°．一质进为1kg的滑块从AU斜面上由静止开始下滑，不计滑块经过连接处B的能量损失，从 滑块滑上水平面BC开始计时，其运动的图象如图乙所示．重力加速度g取10m/s2，已知sin37°=0.6，cos37°=0.8．试求：
