题目内容
(2006?海淀区二模)匀强磁场中有一个静止的放射性同位素铝核
Al放出α粒子(即
He)后,产生的反冲核Y(即
Na)和α粒子分别做匀速圆周运动,不计粒子所受的重力及粒子间的相互作用.则( )
28 13 |
4 2 |
24 11 |
分析:放射性元素衰变过程动量守恒,由动量守恒定律判断出反冲核Y和α粒子动量关系.两个粒子在匀强磁场中做匀速圆周运动时,由洛伦兹力提供向心力,由半径公式r=
、周期公式T=
分析研究,式中mv是动量的大小.
| mv |
| qB |
| 2πm |
| qB |
解答:解:A、反冲核Y和α粒子做匀速圆周运动,都由洛伦兹力提供向心力,半径为r=
在衰变过程中,遵守动量守恒定律,原来铝核
Al处于静止状态,动量为零,则衰变后放出的反冲核Y和α粒子运量大小相等、方向相反.公式r=
中mv是粒子的动量,则知反冲核Y和α粒子的半径与电荷量成反比,为rY:rα=qα:qY=2e:11e=2:11.故A错误.
B、因两个粒子的动量大小相等,由动量P=mv,知反冲核Y和α粒子做匀速圆周运动的速率之比与质量成反比,即为4:24=1:6.故B错误.
C、粒子做匀速圆周运动的周期T=
,周期与两个粒子的比荷成反比,故周期之比为TY:Tα=
:
=
:
=
.故C错误.
D、由r=
、动能Ek=
mv2,得Ek=
,得动能之比EkY:Ekα=
?r
:
?
=1:6.故D正确.
故选D
| mv |
| qB |
在衰变过程中,遵守动量守恒定律,原来铝核
28 13 |
| mv |
| qB |
B、因两个粒子的动量大小相等,由动量P=mv,知反冲核Y和α粒子做匀速圆周运动的速率之比与质量成反比,即为4:24=1:6.故B错误.
C、粒子做匀速圆周运动的周期T=
| 2πm |
| qB |
| qα |
| mα |
| qY |
| mY |
| 2 |
| 4 |
| 11 |
| 24 |
| 12 |
| 11 |
D、由r=
| mv |
| qB |
| 1 |
| 2 |
| q2B2r2 |
| 2m |
| ||
| mY |
2 Y |
| ||
| mα |
| r | 2 α |
故选D
点评:放射性元素放射后,两带电粒子的动量是守恒.正好轨迹的半径公式中也有动量的大小,所以可以研究半径与电荷数的关系.

练习册系列答案
相关题目
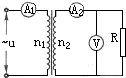 (2006?海淀区二模)如图1所示,一理想变压器原线圈的匝数为n1=1100匝,副线圈匝数n2=180匝,交流电源的电压u=220
(2006?海淀区二模)如图1所示,一理想变压器原线圈的匝数为n1=1100匝,副线圈匝数n2=180匝,交流电源的电压u=220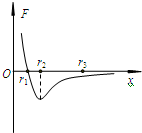 (2006?海淀区二模)将甲分子固定在坐标原点O,乙分子位于x轴上.甲、乙分子间作用力与距离关系的函数图象如图所示.若把乙分子从r3处由静止释放,则仅在分子力作用下,( )
(2006?海淀区二模)将甲分子固定在坐标原点O,乙分子位于x轴上.甲、乙分子间作用力与距离关系的函数图象如图所示.若把乙分子从r3处由静止释放,则仅在分子力作用下,( ) (2006?海淀区二模)利用光电管研究光电效应实验原理示意图如图3所示,用可见光照射阴极K,电流表中有电流通过,则( )
(2006?海淀区二模)利用光电管研究光电效应实验原理示意图如图3所示,用可见光照射阴极K,电流表中有电流通过,则( )