题目内容
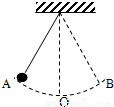
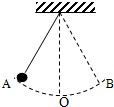如图，小球在关于O点对称的AB两点间摆动，最高点时与竖直方向夹角为30°，试求：
（1）小球做圆周运动的向心力由哪些力提供？
（2）若摆线的长度R，小球质量为m，小球在最低点O的速度为v，求小球在O点时受到绳子的拉力多大？小球在B点时绳子的拉力多大？
解：（1）小球做圆周运动的向心力由绳子的拉力与重力在法向的分力的合力提供．
（2）在O点，由牛顿第二定律得
F-mg=m
则绳子拉力为 F=mg+m
在B 点，由平衡条件得绳子拉力为
F′-mgscos30°=0
得F′=
mg
答：（1）小球做圆周运动的向心力由绳子的拉力与重力在法向的分力的合力提供．
（2）小球在O点时受到绳子的拉力为mg+m，小球在B点时绳子的拉力为mg．
分析：（1）分析小球的受力情况，小球的向心力由绳子的拉力与重力在法向的分力的合力提供；
（2）小球在O点时，根据牛顿第二定律列方程求解绳子的拉力大小．小球在B点时，速度为零，由平衡条件求解绳子的拉力大小．
点评：本题要掌握圆周运动的向心力是由指向圆心的合力提供，根据牛顿第二定律求解绳子拉力的大小．
（2）在O点，由牛顿第二定律得
F-mg=m
则绳子拉力为 F=mg+m
在B 点，由平衡条件得绳子拉力为
F′-mgscos30°=0
得F′=
mg 答：（1）小球做圆周运动的向心力由绳子的拉力与重力在法向的分力的合力提供．
（2）小球在O点时受到绳子的拉力为mg+m
，小球在B点时绳子的拉力为mg．分析：（1）分析小球的受力情况，小球的向心力由绳子的拉力与重力在法向的分力的合力提供；
（2）小球在O点时，根据牛顿第二定律列方程求解绳子的拉力大小．小球在B点时，速度为零，由平衡条件求解绳子的拉力大小．
点评：本题要掌握圆周运动的向心力是由指向圆心的合力提供，根据牛顿第二定律求解绳子拉力的大小．
练习册系列答案
相关题目
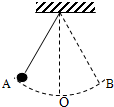如图，小球在关于O点对称的AB两点间摆动，最高点时与竖直方向夹角为30°，试求：
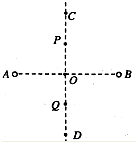如图所示，两等量同种点电荷固定在水平方向上的A、B两点，过AB中点O的竖直方向上有C、P、Q、D四点，其中C、D和P、Q分别关于O点对称．一带电小球自C点由静止释放，运动到P点时小球的加速度为零．重力加速度为g，则下列判断正确的是（ ）
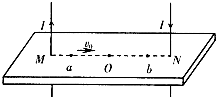如图所示，两根长直导线竖直插入光滑绝缘水平桌面上的M、N两小孔中，O为M、N连线中点，连线上a、b两点关于O点对称．导线通有大小相等、方向相反的电流．已知通电长直导线在周围产生的磁场的磁感应强度B=