Question

【题目】如图所示，AB是两块折射率不同，外形完全相同的光学介质，其横截面为直角三角形，较小的直角边的边长为d，对应的锐角为α=300；现将两块介质结合在一起，恰好构成一个长方形；然后将一束光从图示长方形上某点以入射角θ=450射入介质A，该光经折射后进入介质B时，恰好经过斜边中点且能沿之前传播，最后该光从介质B的下表面射出；已知出射光线与界面的夹角为300，光在真空中的光速为c，求

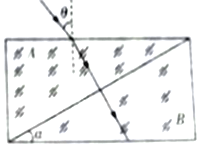
①介质AB的折射率.

②该光在介质B内传播的时间。

Answer 1

【答案】①②

【解析】①由于AB两块介质的折射率不同，且光在长方形介质内沿直线传播，说明折射光一定与AB分界面垂直，如图所示，由几何关系可知，光进入介质A的折射角为α=300，由折射定律 ,

解得

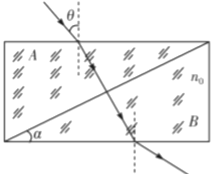
②根据题意可知，由几何关系知道，光在介质B中的入射角 ,出射角i=600，

由折射定律

解得：

由折射定律可知

光经过斜边中点进入B介质，所以光在B介质中的传播距离为

光在介质B中的传播时间 联立可得：