题目内容
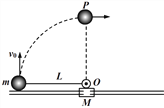
【题目】如图甲所示，将一质量分布均匀的长木板静止放在光滑的水平面上，一个小滑块（可视为质点）以水平初速度v0=6 m/s，由木板左端向右滑动，到达右端时恰能与木板保持相对静止。已知长木板的质量是小滑块质量的2倍，小滑块和长木板之间的动摩擦因素
，g取10 m/s2。求：
（1）小滑块到达长木板右端时的速度大小v；
（2）长木板的长度L；
（3）若将长木板分成等长的两段A、B，并紧挨着放在原水平面上，如图乙所示。让小滑块仍以初速度v0=6 m/s由A的左端开始向右滑动，求小滑块最终离B的右端的距离
。
【答案】（1）
（2）
（3）
【解析】解：（1）设小滑块的质量为m，长木板的质量为2m，由动量守恒定律得：
代入数据解得， 
（2）由功能关系得：
代入数据解得， 
（3）设小滑块刚滑上木板B左端时的速度为v1,木板A、B的速度为v2。小滑块相对B静止时，速度为
，由动量守恒定律和功能关系可得：
代入数据联立解得， 
练习册系列答案
相关题目
