题目内容
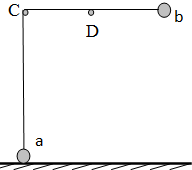 如图所示,一根不可伸长的轻绳两端各系一个小球a和b,跨在两根固定在同一高度的光滑水平细杆C和D上,质量为ma的a球置于地面上,质量为mb的b球从水平位置静止释放.当b球摆过的角度为90°时,a球对地面压力刚好为零,下列结论正确的是( )
如图所示,一根不可伸长的轻绳两端各系一个小球a和b,跨在两根固定在同一高度的光滑水平细杆C和D上,质量为ma的a球置于地面上,质量为mb的b球从水平位置静止释放.当b球摆过的角度为90°时,a球对地面压力刚好为零,下列结论正确的是( )分析:b球摆动过程中运用机械能守恒求出在最低点的速度.
根据牛顿运动定律和向心力公式求出绳子的拉力,再去进行比较.
根据牛顿运动定律和向心力公式求出绳子的拉力,再去进行比较.
解答:解:A、B、由于b球摆动过程中机械能守恒,则有
mbgl=
mbv2,
当b球摆过的角度为90°时,a球对地面压力刚好为零,说明此时绳子张力为mag,
根据牛顿运动定律和向心力公式得
mag-mbg=mb
,
解得:ma:mb=3:1,故A正确,B错误.
C、D、由上述求解过程可以看出,
F-mbg=mb
=3mbg
所以球到悬点的距离跟最终结果无关,故C错误,故D正确.
故选AD.
mbgl=
| 1 |
| 2 |
当b球摆过的角度为90°时,a球对地面压力刚好为零,说明此时绳子张力为mag,
根据牛顿运动定律和向心力公式得
mag-mbg=mb
| v2 |
| l |
解得:ma:mb=3:1,故A正确,B错误.
C、D、由上述求解过程可以看出,
F-mbg=mb
| v2 |
| l′ |
所以球到悬点的距离跟最终结果无关,故C错误,故D正确.
故选AD.
点评:本题关键对小球b运用机械能守恒定律和向心力公式联合列式求解.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
