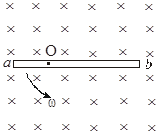题目内容
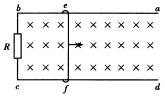
(20分)足够长的平行金属导轨ab、cd放置在水平面上,处在磁感应强度B=1.00T的竖直方向的匀强磁场中,导轨间连接阻值为R=0.30Ω的电阻,质量m=0.5kg的金属棒ef与bc紧贴在导轨上,处于两导轨间的长度L=0.40m、电阻r=0.10Ω,如图所示。在水平恒力F作用下金属棒ef由静止开始向右运动,其运动距离与时间的关系如下表所示。导轨与金属棒ef间的动摩擦因数为0.3,导轨电阻不计,g=10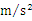 求:
求:
(1)在4.0s时间内,通过金属棒截面的电荷量q;
(2)水平恒力F;
(3)庆丰同学在计算7.0s时间内,整个回路产生的焦耳热Q时,是这样计算的:
先算7.0s内的电荷量
再算电流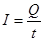
再用公式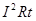 计算出焦耳热
计算出焦耳热
请你简要分析这样做是否正确?认为正确的,请算出结果;认为错误的,请用自己的方法算出7.0s,整个回路产生的焦耳热Q。
 求:
求:
| 时间t(s) | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 |
| 运动距离x(m) | 0.0 | 0.6 | 2.0 | 4.3 | 6.8 | 9.3 | 11.8 | 14.3 |
(2)水平恒力F;
(3)庆丰同学在计算7.0s时间内,整个回路产生的焦耳热Q时,是这样计算的:
先算7.0s内的电荷量
再算电流
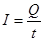
再用公式
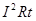 计算出焦耳热
计算出焦耳热请你简要分析这样做是否正确?认为正确的,请算出结果;认为错误的,请用自己的方法算出7.0s,整个回路产生的焦耳热Q。
(1)6.8C (2)2.5N (3)12.7J
试题分析:(1).金属棒产生的平均感应电动势
 (1分)
(1分)平均电流
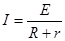 (1分)
(1分)电荷量
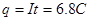 (2分)
(2分)(2).由表中数据可知3.0s以后棒ef做匀速直线运动
 (2分)
(2分)F-f=BIL (2分)
由
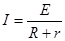 , E= BLv (2分)
, E= BLv (2分)解得F="BIL+" f=2.5N (3分)
(3)庆丰同学用电流的平均值计算焦耳热是错误的, (2分)
根据能量转化和守恒定律有
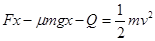 (3分)
(3分)解得Q=12.7J (2分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
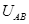 ; (3).在0~4s内,通过R的电量
; (3).在0~4s内,通过R的电量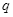 .
.
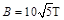 的匀强磁场,定值电阻R=1Ω。把质量为m=1kg、电阻不计的金属杆从距b、e高h=1m的导轨上静止释放,杆在直轨道上先加速后匀速下滑。如果杆与木板间摩擦因数μ=0.2,取g=10m/s2,求:
的匀强磁场,定值电阻R=1Ω。把质量为m=1kg、电阻不计的金属杆从距b、e高h=1m的导轨上静止释放,杆在直轨道上先加速后匀速下滑。如果杆与木板间摩擦因数μ=0.2,取g=10m/s2,求: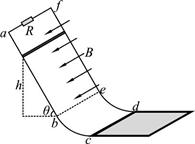
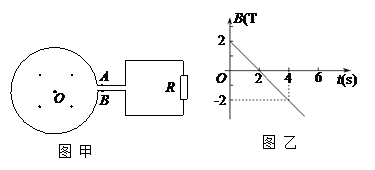
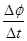 、通过金属棒的电荷量q以及a、b两端的电势差U随时间t变化的图象中,正确的是
、通过金属棒的电荷量q以及a、b两端的电势差U随时间t变化的图象中,正确的是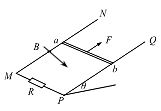
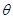 ,轨道间接有电动势为E(内阻不计)的电源,现将一根质量为m、电阻为R的金属杆ab水平且与轨道垂直放置在轨道上,金属杆与轨道接触摩擦和电阻均不计,整个装置处在匀强磁场(磁场垂直于金属棒)中且ab杆静止在轨道上,求:
,轨道间接有电动势为E(内阻不计)的电源,现将一根质量为m、电阻为R的金属杆ab水平且与轨道垂直放置在轨道上,金属杆与轨道接触摩擦和电阻均不计,整个装置处在匀强磁场(磁场垂直于金属棒)中且ab杆静止在轨道上,求:
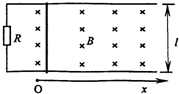
 ,宽
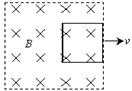
,宽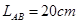 ,竖直放置在水平面上。中间有一磁感应强度B=1.0T,磁场宽度
,竖直放置在水平面上。中间有一磁感应强度B=1.0T,磁场宽度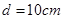 的匀强磁场。线框在水平向右的恒力F=2N的作用下,从图示位置由静止开始沿水平方向运动,线框AB边从左侧进入磁场,从磁场右侧以
的匀强磁场。线框在水平向右的恒力F=2N的作用下,从图示位置由静止开始沿水平方向运动,线框AB边从左侧进入磁场,从磁场右侧以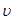 =1m/s的速度匀速运动离开磁场,整个过程中线框始终受到大小恒定的阻力Ff=1N,且线框不发生转动。求线框的AB边:
=1m/s的速度匀速运动离开磁场,整个过程中线框始终受到大小恒定的阻力Ff=1N,且线框不发生转动。求线框的AB边: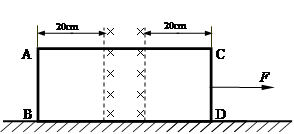
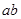 长为
长为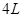 ,匀强磁场的磁感应强度为
,匀强磁场的磁感应强度为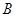 ,导体绕过
,导体绕过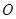 点垂直纸面的轴以角速度
点垂直纸面的轴以角速度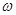 匀速转动,
匀速转动,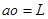 .则
.则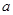 端和
端和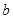 端的电势差
端的电势差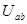 的大小等于
的大小等于