题目内容
6.一列简谐横波在某一时刻t1的波形如图实线所示,t2时刻的波形如图虚线所示,已知t=t2-t1=0.5s求这列波的传播速度是多大?
分析 若波向右传播,传播的时间为(n+$\frac{1}{4}$)•T,若波向左传播,传播的时间为(n+$\frac{3}{4}$)•T,根据波的周期性:相隔整数倍周期的时间,波形相同,根据时间与周期关系的通项,求出周期,再求解波速.
解答 解:若波向右传播,则有:
(n+$\frac{1}{4}$)•T=t
则得:T=$\frac{4t}{4n+1}$=$\frac{4×0.5}{4n+1}$=$\frac{2}{4n+1}$,(n=0,1,2,…);
该波的波长为 λ=8m
则波速为 v=$\frac{λ}{T}$=4(4n+1)(m/s)(n=0,1,2,…);
若波向左传播,则有:
(n+$\frac{3}{4}$)T=t
则得:T=$\frac{4t}{4n+3}$=$\frac{2}{4n+3}$,(n=0,1,2,…);
波速为:v=$\frac{λ}{T}$=4(4n+3)(n=0,1,2,…);
答:这列波的传播速度是4(4n+1)(m/s)或4(4n+3)(m/s),(n=0,1,2,…).
点评 本题是波动图象中典型的问题,要根据波的周期性和双向性研究传播时间与周期的关系,是多解问题,不能漏解.要有运用数学知识分析和解决物理问题的能力.

练习册系列答案
相关题目
8. 如图所示,一个有界匀强磁场区域,磁场方向垂直纸面向外,一个矩形闭合线圈abcd,沿纸面由位置1运动到位置2,则( )
如图所示,一个有界匀强磁场区域,磁场方向垂直纸面向外,一个矩形闭合线圈abcd,沿纸面由位置1运动到位置2,则( )
 如图所示,一个有界匀强磁场区域,磁场方向垂直纸面向外,一个矩形闭合线圈abcd,沿纸面由位置1运动到位置2,则( )
如图所示,一个有界匀强磁场区域,磁场方向垂直纸面向外,一个矩形闭合线圈abcd,沿纸面由位置1运动到位置2,则( )| A. | 线圈进入磁场过程中,线圈中有感应电流 | |
| B. | 线圈完全进入磁场,且线圈做匀速运动,线圈中有感应电流 | |
| C. | 线圈完全进入磁场,且线圈做加速运动,线圈中有感应电流 | |
| D. | 线圈离开磁场过程中,线圈中有感应电流 |
1.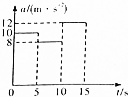 一质点在0~15s内竖直向上运动,其加速度一时间(a-t)图象如图所示,若取竖直向下为正方向,重力加速度g取10m/s2,则下列说法正确的是( )
一质点在0~15s内竖直向上运动,其加速度一时间(a-t)图象如图所示,若取竖直向下为正方向,重力加速度g取10m/s2,则下列说法正确的是( )
 一质点在0~15s内竖直向上运动,其加速度一时间(a-t)图象如图所示,若取竖直向下为正方向,重力加速度g取10m/s2,则下列说法正确的是( )
一质点在0~15s内竖直向上运动,其加速度一时间(a-t)图象如图所示,若取竖直向下为正方向,重力加速度g取10m/s2,则下列说法正确的是( )| A. | 质点的机械能不断增加 | |
| B. | 在0~5s内质点发生的位移为125m | |
| C. | 在10~15s内质点的机械能一直增加 | |
| D. | 在t=15s时质点的机械能大于t=5s时质点的机械能 |
11.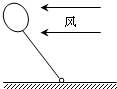 在广场游玩时,一小孩将一充有氢气的气球用细绳系于一个小石块上,并将小石块静止置于水平地面上,如图所示.风沿水平方向吹,气球受到的风力f=kS2v(k是阻力系数,S是迎风横截面积,v是风速).若水平的风速逐渐增大(设空气密度不变,气球所受的空气浮力不变),则下列说法中正确的是( )
在广场游玩时,一小孩将一充有氢气的气球用细绳系于一个小石块上,并将小石块静止置于水平地面上,如图所示.风沿水平方向吹,气球受到的风力f=kS2v(k是阻力系数,S是迎风横截面积,v是风速).若水平的风速逐渐增大(设空气密度不变,气球所受的空气浮力不变),则下列说法中正确的是( )
 在广场游玩时,一小孩将一充有氢气的气球用细绳系于一个小石块上,并将小石块静止置于水平地面上,如图所示.风沿水平方向吹,气球受到的风力f=kS2v(k是阻力系数,S是迎风横截面积,v是风速).若水平的风速逐渐增大(设空气密度不变,气球所受的空气浮力不变),则下列说法中正确的是( )
在广场游玩时,一小孩将一充有氢气的气球用细绳系于一个小石块上,并将小石块静止置于水平地面上,如图所示.风沿水平方向吹,气球受到的风力f=kS2v(k是阻力系数,S是迎风横截面积,v是风速).若水平的风速逐渐增大(设空气密度不变,气球所受的空气浮力不变),则下列说法中正确的是( )| A. | 细绳的拉力变大 | |
| B. | 地面受到小石块的压力逐渐减小 | |
| C. | 小石块滑动前受到地面施加的摩擦力逐渐增大 | |
| D. | 小石块有可能连同气球一起被吹离地面 |
15. 如图所示,某同学用1m长的轻绳拉着质量为0.1kg的小球在水平面内做匀速圆周运动,开始时轻绳与竖直方向的夹角为37°,改变拉力的作用,最后小球在水平面内做匀速圆周运动时,轻绳与竖直方向的夹角为53°,不计空气阻力的作用,手的位置不变(已知sin37°=0.6,cos37°=0.8,g=10m/s2.结果保留1位有效数字),则下列说法正确的是( )
如图所示,某同学用1m长的轻绳拉着质量为0.1kg的小球在水平面内做匀速圆周运动,开始时轻绳与竖直方向的夹角为37°,改变拉力的作用,最后小球在水平面内做匀速圆周运动时,轻绳与竖直方向的夹角为53°,不计空气阻力的作用,手的位置不变(已知sin37°=0.6,cos37°=0.8,g=10m/s2.结果保留1位有效数字),则下列说法正确的是( )
 如图所示,某同学用1m长的轻绳拉着质量为0.1kg的小球在水平面内做匀速圆周运动,开始时轻绳与竖直方向的夹角为37°,改变拉力的作用,最后小球在水平面内做匀速圆周运动时,轻绳与竖直方向的夹角为53°,不计空气阻力的作用,手的位置不变(已知sin37°=0.6,cos37°=0.8,g=10m/s2.结果保留1位有效数字),则下列说法正确的是( )
如图所示,某同学用1m长的轻绳拉着质量为0.1kg的小球在水平面内做匀速圆周运动,开始时轻绳与竖直方向的夹角为37°,改变拉力的作用,最后小球在水平面内做匀速圆周运动时,轻绳与竖直方向的夹角为53°,不计空气阻力的作用,手的位置不变(已知sin37°=0.6,cos37°=0.8,g=10m/s2.结果保留1位有效数字),则下列说法正确的是( )| A. | 合力对小球做的功为0.2J | B. | 小球的重力势能增加了0.2J | ||
| C. | 小球的机械能增加了0.5J | D. | 人对小球做的功为0.3J |
16.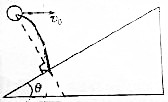 如图所示.小球以v0正对倾角为θ的斜面水平抛出,若小球到达斜面的位移最小,重力加速度为g,则( )
如图所示.小球以v0正对倾角为θ的斜面水平抛出,若小球到达斜面的位移最小,重力加速度为g,则( )
 如图所示.小球以v0正对倾角为θ的斜面水平抛出,若小球到达斜面的位移最小,重力加速度为g,则( )
如图所示.小球以v0正对倾角为θ的斜面水平抛出,若小球到达斜面的位移最小,重力加速度为g,则( )| A. | 小球飞行时间为:$\frac{2{v}_{0}}{gtanθ}$ | |
| B. | 飞行高度$\frac{2{{v}_{0}}^{2}ta{n}^{2}θ}{g}$ | |
| C. | 飞行的水平距离为$\frac{{{v}_{0}}^{2}}{gtanθ}$ | |
| D. | 若小球速度适当变小可能垂直打在斜面上 |
 如图所示,PN和MQ两板平行且板间存在垂直纸面向里的匀强磁场,两板间距离及PN和MQ长均为d,一带正电的质子从PN板的正中间O点以速度v0垂直射入磁场,为使质子能射出两板间,试求磁感应强度B的大小.已知质子带电荷量为e,质量为m.
如图所示,PN和MQ两板平行且板间存在垂直纸面向里的匀强磁场,两板间距离及PN和MQ长均为d,一带正电的质子从PN板的正中间O点以速度v0垂直射入磁场,为使质子能射出两板间,试求磁感应强度B的大小.已知质子带电荷量为e,质量为m.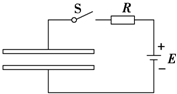 两块大小、形状完全相同的金属板平行放置,构成一平行板电容器,与它相连接的电路如图所示,闭合开关S,电源即给电容器充电.
两块大小、形状完全相同的金属板平行放置,构成一平行板电容器,与它相连接的电路如图所示,闭合开关S,电源即给电容器充电.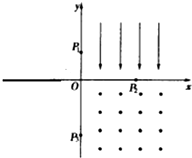 如图所示,在第一象限的空间中存在匀强电场,场强沿y轴负方向;在第四象限中,存在匀强磁场,磁场方向垂直xy平面(纸面)向外.一电量为q、质量为m的带正电的运动粒子,经过y轴上y=h处的点P1时速率为v0,方向沿x轴正方向;然后经过x轴上x=2h处的P2点进入磁场,并经过y轴上y=-2h处的P3点,最后达到x轴上的P4点(图中未画出).若不计重力,求:
如图所示,在第一象限的空间中存在匀强电场,场强沿y轴负方向;在第四象限中,存在匀强磁场,磁场方向垂直xy平面(纸面)向外.一电量为q、质量为m的带正电的运动粒子,经过y轴上y=h处的点P1时速率为v0,方向沿x轴正方向;然后经过x轴上x=2h处的P2点进入磁场,并经过y轴上y=-2h处的P3点,最后达到x轴上的P4点(图中未画出).若不计重力,求: