题目内容
11．关于质点，以下说法中正确的是（ ）| A． | 凡是体积非常小的物体，都可以看作是质点 | |
| B． | 凡是体积特别大的物体，一定不能看作质点 | |
| C． | 研究电子的自旋时，由于电子很小可看作是质点 | |
| D． | 研究地球公转时，地球可以看成是质点 |
分析 质点是只计质量、不计大小、形状的一个几何点，是实际物体在一定条件的科学抽象，能否看作质点与物体本身无关，要看所研究问题的性质，看物体的形状和大小在所研究的问题中是否可以忽略
解答 解：A、体积很小的物体不一定能看做质点，比如原子体积很小，在研究原子内部结构的时候是不能看成质点的，所以A错误．
B、体积很大的物体有时也能看成质点，如地球体积很大，在研究其绕太阳的公转时，由于地球到太阳的距离比地球本身尺寸大很多，可以看作质点，所以B错误；
C、研究电子的自旋时，电子不可看作是质点，看作质点后，没有形状、没有体积，则研究无法进行，所以C错误；
D、由B分析可得，所以D正确．
故选：D
点评 质点是运动学中一个重要概念，要理解其实质，不能停在表面．一般自转的物体不可以看作质点，平动的物体可以看作质点．
练习册系列答案
相关题目
1．
在做探究弹力和弹簧伸长的关系的实验中，实验装置如图．所用的每只钩码质量都是30g，先测出不挂钩码时弹簧的自然长度，再将5个钩码逐个挂在弹簧的下端，每次测出相应的弹簧总长度，将数据填入表中．（弹力未超过弹性限度，取g=9.8m/s2）
（1）试根据这些实验数据在如图给定的坐标纸上作出弹簧所受弹力大小F跟弹簧总长l之间的函数关系图线，说明图线跟坐标轴交点的物理意义．
（2）上一问所得图线的物理意义是什么？该弹簧的劲度k是多大？
在做探究弹力和弹簧伸长的关系的实验中，实验装置如图．所用的每只钩码质量都是30g，先测出不挂钩码时弹簧的自然长度，再将5个钩码逐个挂在弹簧的下端，每次测出相应的弹簧总长度，将数据填入表中．（弹力未超过弹性限度，取g=9.8m/s2）| 砝码质量（g） | 0 | 30 | 60 | 90 | 120 | 150 |
| 弹簧总长（cm） | 6.00 | 7.15 | 8.34 | 9.48 | 10.64 | 11.79 |
| 弹力大小（N） |
（2）上一问所得图线的物理意义是什么？该弹簧的劲度k是多大？
2．
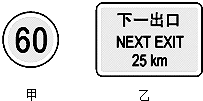为了使公路交通有序、安全，道路两旁都竖立了许多交通标志．如图所示，甲图是广州市环市路高架桥上的限速标志（白底、红圈、黑字），表示允许行驶的最大速度是60km/h；乙图是路线指示标志，表示离下一出口还有25km．上述两个数据的物理意义是（ ）
为了使公路交通有序、安全，道路两旁都竖立了许多交通标志．如图所示，甲图是广州市环市路高架桥上的限速标志（白底、红圈、黑字），表示允许行驶的最大速度是60km/h；乙图是路线指示标志，表示离下一出口还有25km．上述两个数据的物理意义是（ ）| A． | 60km/h是平均速度 | B． | 60km/h是瞬时速度 | ||
| C． | 25km是位移 | D． | 25km是路程 |
19．关于平抛运动，以下说法正确的是（ ）
| A． | 平抛运动是加速度恒等于g的匀变速运动 | |
| B． | 平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动 | |
| C． | 平抛物体在空间运动的时间与物体抛出的速度无关，只取决于抛出点的高度 | |
| D． | 平抛物体的水平位移，与抛出点高度无关，只取决于水平抛出的速度 |
6．
如图，轻绳上端固定，下端系一小球，悬点正下方固定一钉子，小球从A点开始下摆，轻绳碰到钉子后，钉子之上的轻绳不再摆动．轻绳碰到钉子后一瞬与碰到钉子前一瞬相比，（ ）
如图，轻绳上端固定，下端系一小球，悬点正下方固定一钉子，小球从A点开始下摆，轻绳碰到钉子后，钉子之上的轻绳不再摆动．轻绳碰到钉子后一瞬与碰到钉子前一瞬相比，（ ）| A． | 小球的速度突然增大了 | B． | 小球的角速度突然增大了 | ||
| C． | 小球的加速度突然增大了 | D． | 轻绳的对小球的拉力突然增大了 |
16．已知某单色光的波长为λ，在真空中的光速为c，普朗克常量为h，则该单色光的能量子为（ ）
| A． | $\frac{hc}{λ}$ | B． | $\frac{hλ}{c}$ | C． | $\frac{h}{λ}$ | D． | hcλ |
3．
2014年8月，山东鲁能队再度包揽乒超男女团体的冠军，加冕双冠王!假设运动员在训练中手持乒乓球拍托球沿水平面做匀加速跑动，球拍与球保持相对静止且球拍平面和水平面之间夹角为θ．设球拍和球质量分别为M、m，不计球拍和球之间摩擦，不计空气阻力，则（ ）
2014年8月，山东鲁能队再度包揽乒超男女团体的冠军，加冕双冠王!假设运动员在训练中手持乒乓球拍托球沿水平面做匀加速跑动，球拍与球保持相对静止且球拍平面和水平面之间夹角为θ．设球拍和球质量分别为M、m，不计球拍和球之间摩擦，不计空气阻力，则（ ）| A． | 运动员的加速度大小为gsinθ | |
| B． | 球拍对球的作用力大小为mgcosθ | |
| C． | 运动员对球拍的作用力大小为$\frac{（M+m）g}{cosθ}$ | |
| D． | 运动员对地面的作用力方向竖直向下 |
19．
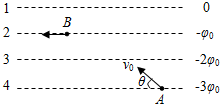如图所示，在匀强磁场中有四条间距均为d的平行等势线1、2、3、4，各条线上的电势分别为：0、-φ0、-2φ0、-3φ0；有一个带电粒子，质量为m（不计重力），电荷量为q，从A点与等势线4成θ角以速度v0射入电场中，到达等势线2上的B点时，速度方向恰好水平向左，则匀强电场场强的大小为（ ）
如图所示，在匀强磁场中有四条间距均为d的平行等势线1、2、3、4，各条线上的电势分别为：0、-φ0、-2φ0、-3φ0；有一个带电粒子，质量为m（不计重力），电荷量为q，从A点与等势线4成θ角以速度v0射入电场中，到达等势线2上的B点时，速度方向恰好水平向左，则匀强电场场强的大小为（ ）| A． | $\frac{m{{v}_{0}}^{2}si{n}^{2}θ}{4qd}$ | B． | $\frac{m{{v}_{0}}^{2}si{n}^{2}θ}{2qd}$ | C． | $\frac{m{{v}_{0}}^{2}co{s}^{2}θ}{4qd}$ | D． | $\frac{m{{v}_{0}}^{2}co{s}^{2}θ}{2qd}$ | ||||
| E． | $\frac{m{{v}_{0}}^{2}si{n}^{2}θ}{4qd}$ |