题目内容
8. 如图所示,在x-o-y坐标系中,以(r,0)为圆心、r为半径的圆形区域内存在匀强磁场,磁场的磁感应强度大小为B,方向垂直于纸面向里.在y>r的足够大的区域内,存在沿y轴负方向的匀强电场,场强大小为E.从O点以相同速率向不同方向发射质子,质子的运动轨迹均在纸面内,且质子在磁场中运动的轨迹半径也为r.已知质子的电荷量为q,质量为m,不计质子所受重力及质子间相互作用力的影响.
如图所示,在x-o-y坐标系中,以(r,0)为圆心、r为半径的圆形区域内存在匀强磁场,磁场的磁感应强度大小为B,方向垂直于纸面向里.在y>r的足够大的区域内,存在沿y轴负方向的匀强电场,场强大小为E.从O点以相同速率向不同方向发射质子,质子的运动轨迹均在纸面内,且质子在磁场中运动的轨迹半径也为r.已知质子的电荷量为q,质量为m,不计质子所受重力及质子间相互作用力的影响.(1)求质子射入磁场时速度的大小;
(2)若质子沿x轴正方向射入磁场,求质子从O点进入磁场到第二次离开磁场经历的时间;
(3)若质子沿与x轴正方向成夹角θ的方向从O点射入第一象限的磁场中,求质子在磁场中运动的总时间.
分析 (1)粒子在磁场中运动靠洛伦兹力提供向心力,通过轨道半径,根据牛顿第二定律求出粒子射入磁场的速度.
(2)粒子沿x轴正向射入磁场后,在磁场中运动了$\frac{1}{4}$个圆周后,以速度v逆着电场方向进入电场,原路径返回后,再射入磁场,在磁场中运动了$\frac{1}{4}$个圆周后离开磁场.求出粒子在磁场中运动的周期,从而求出粒子磁场中运动的时间,根据牛顿第二定律结合运动学公式求出粒子在电场中运动的时间,从而得出最终的总时间.
(3)结合作图,找出运动轨迹,然后求解出时间
解答 解:(1)质子射入磁场后做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
qvB=m$\frac{{v}^{2}}{r}$,
解得:v=$\frac{qBr}{m}$;
(2)质子沿x轴正向射入磁场后,在磁场中运动了$\frac{1}{4}$个圆周后,以速度υ逆着电场方向进入电场,原路径返回后,再射入磁场,在磁场中运动了$\frac{1}{4}$个圆周后离开磁场.
在磁场中运动周期:T=$\frac{2πm}{qB}$,
质子在磁场中运动的时间:t1=$\frac{1}{2}$T=$\frac{πm}{qB}$,
进入电场后做匀变速直线运动,加速度大小:a=$\frac{qE}{m}$,
质子在电场中运动的时间:t2=$\frac{2v}{a}$=$\frac{2Br}{E}$,
所求时间为:t=t1+t2=$\frac{πm}{qB}$+$\frac{2Br}{E}$;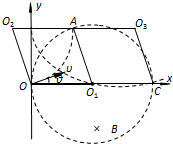 (3)当质子沿与x轴正方向成夹角θ的方向从第一象限射入磁场时,设质子将从A点射出磁场,如图所示:
(3)当质子沿与x轴正方向成夹角θ的方向从第一象限射入磁场时,设质子将从A点射出磁场,如图所示:
其中O1、O2分别为磁场区域圆和质子轨迹圆的圆心.
由于轨迹圆的半径等于磁场区域圆的半径,所以OO1AO2为菱形,即AO2平行x轴,说明质子以平行y轴的速度离开磁场,也以沿y轴负方向的速度再次进入磁场,有:
∠O2=90°-θ.
所以,质子第一次在磁场中运动的时间:t1′=$\frac{90°-θ}{360°}$T,
此后质子轨迹圆的半径依然等于磁场区域圆的半径,设质子将从C点再次射出磁场.
如图所示,其中O1、O3分别为磁场区域圆和质子轨迹圆的圆心,AO3平行x轴.
由于O1AO3C为菱形,即CO1平行AO3,即平行x轴,说明C就是磁场区域圆与x轴的交点.
这个结论与θ无关.所以,OO2O3C为平行四边形,∠O3=90°+θ
质子第二次在磁场中运动的时间为:t2′=$\frac{90°+θ}{360°}$T,
质子在磁场中运动的总时间:t′=t1′+t2′=$\frac{1}{2}$T=$\frac{πm}{qB}$;
答:(1)质子射入磁场时速度的大小为$\frac{qBr}{m}$;
(2)若质子沿x轴正方向射入磁场,质子从O点进入磁场到第二次离开磁场经历的时间为$\frac{πm}{qB}$+$\frac{2Br}{E}$;
(3)若质子沿与x轴正方向成夹角θ的方向从O点射入第一象限的磁场中,质子在磁场中运动的总时间为$\frac{πm}{qB}$.
点评 本题考查了粒子在匀强磁场和匀强电场中的运动,关键是理清粒子的运动规律,在磁场中做匀速圆周运动,进入电场速度方向与电场方向平行,先做匀减速直线运动,返回做匀加速直线运动.

 高效智能课时作业系列答案
高效智能课时作业系列答案
| A. | 0~ta段火箭的加速度小于ta~tb段火箭的加速度 | |
| B. | 0~tb段火箭是上升的,tb~tc段火箭是下落的 | |
| C. | tb时刻火箭的速度最大 | |
| D. | tc时刻火箭回到地面 |
 如图所示,条形磁铁静止在水平桌面上,闭合铝环从条形磁铁的正上方附近由静止竖直下落至桌面.则在下落过程中( )
如图所示,条形磁铁静止在水平桌面上,闭合铝环从条形磁铁的正上方附近由静止竖直下落至桌面.则在下落过程中( )| A. | 下落过程中铝环能产生方向改变的感应电流 | |
| B. | 磁铁对桌面的压力始终大于其自身的重力 | |
| C. | 铝环所受安培力的方向先向上后向下 | |
| D. | 铝环的加速度小于或等于g |

| A. | 质子仅由电场加速 | |
| B. | 质子在电场中被加速,加速电压越高,射出的速率v越大 | |
| C. | D型盒的直径越大,射出的率度v越大 | |
| D. | 质子在磁场中运动的周期随质子速度增大而增大 |
 带电粒子的质量m=1.7×10-27kg,电荷量q=1.6×10-19C,以速度v=3.2×106m/s沿垂直于磁场同时又垂直于磁场边界的方向进入匀强磁场中,磁场的磁感应强度为B=0.17T,磁场的宽度l=$\frac{\sqrt{3}}{10}$m,如图所示(不计带电粒子的重力).
带电粒子的质量m=1.7×10-27kg,电荷量q=1.6×10-19C,以速度v=3.2×106m/s沿垂直于磁场同时又垂直于磁场边界的方向进入匀强磁场中,磁场的磁感应强度为B=0.17T,磁场的宽度l=$\frac{\sqrt{3}}{10}$m,如图所示(不计带电粒子的重力). 某同学为了测定一只约为100Ω的电阻的阻值,采用了如下方法:
某同学为了测定一只约为100Ω的电阻的阻值,采用了如下方法:

 在如图所示的电路中,电容器A的电容CA=30μF,电容器B的电容CB=10μF.在电键K1、K2都是断开的情况下,分别给电容器A、B充电.充电后,M点的电势比N点高5V,O点的电势比P点低5V.然后把K1、K2都接通,接通后M点的电势比N点高( )
在如图所示的电路中,电容器A的电容CA=30μF,电容器B的电容CB=10μF.在电键K1、K2都是断开的情况下,分别给电容器A、B充电.充电后,M点的电势比N点高5V,O点的电势比P点低5V.然后把K1、K2都接通,接通后M点的电势比N点高( )