题目内容
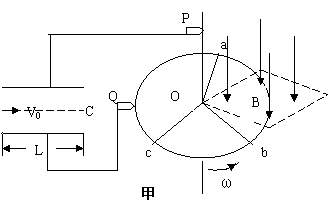
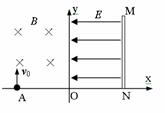
如图21所示,坐标平面的第Ⅰ象限内存在大小为E、方向水平向左的匀强电场,第Ⅱ象限内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场。足够长的挡板MN垂直x轴放置且距原点O的距离为d。一质量为m、带电量为-q的粒子若自距原点O为L的A点以大小为v0,方向沿y轴正方向的速度进入磁场,则粒子恰好到达O点而不进入电场。现该粒子仍从A点进入磁场,但初速度大小为2![]() v0,为使粒子进入电场后能垂直打在挡板上,求粒子(不计重力)在A点第二次进入磁场时:
v0,为使粒子进入电场后能垂直打在挡板上,求粒子(不计重力)在A点第二次进入磁场时:
(1) 其速度方向与x轴正方向之间的夹角。
(2)粒子到达挡板上时的速度大小及打到挡板MN上的位置到x轴的距离.
【解析】设速度为v0时进入磁场后做圆周运动的半径为r
 有
有 ![]() 得r=
得r=![]() =
=![]()
设速度为2![]() v0时进入磁场做圆周运动的半径r′
v0时进入磁场做圆周运动的半径r′
得r′=![]() =
=![]() L
L
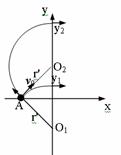
设其速度方向与x轴正方向之间的夹角为θ
由图中的几何关系有:cosθ=![]() =
=![]()
得θ=45°或θ=135°
(2)为使粒子进入电场后能垂直打在挡板上,则要求粒子进入电场时速度方向
与x轴正方向平行,如图所示。粒子进入电场后由动能定理有
qEd=![]() mv′2 -
mv′2 -![]() m(2
m(2![]() v0)2 得v′=
v0)2 得v′=![]()
当θ1=45°时,粒子打到挡板MN上的位置到x轴的距离为
y1=r-r′sin45°=(![]() -1)L
-1)L
当θ2 =135°时,粒子打到挡板MN上的位置到x轴的距离为
y2= r′+ r′sin45°=(![]() +1)L
+1)L
【答案】(1)θ=45°或θ=135° (2)当θ1=45°时,(![]() -1)L;
-1)L;
θ2=135°(![]() +1)L,
+1)L,

 阅读快车系列答案
阅读快车系列答案A.验证机械能守恒定律 B.用单摆测定重力加速度
C.验证动量守恒定律 D.研究平抛物体的运动
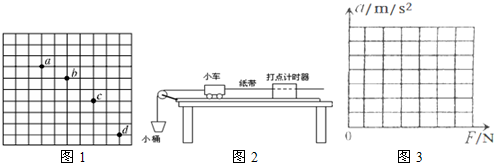
(2)一个小灯泡的额定电压为6.3 V,额定电流约为0.3 A,用以下所给的实验器材描绘出小灯泡的伏安特性曲线。实验电路如图7所示。

电源E1:电动势为8.0 V,内阻不计;
电源E2:电动势为12.0 V,内阻不计;
电压表V:量程为0—10 V,内阻约为10 k Ω;
电流表A1:量程为0—3 A,内阻约为0.1 Ω;
电流表A2:量程为0—300 mA,内阻约为1 Ω;
滑动变阻器R:最大阻值10 Ω,额定电流1.0 A;开关S,导线若干。
①依照实验电路图将图8中的实物图连接成实验电路。
②实验中电源应该选用____________;电流表应该选用_______________。
③实验测出的数据如表2所示,依照这些数据在图9所示的坐标纸中描绘出该小灯泡的伏安特性曲线。
表2
U/V | 0 | 0.5 | 0.8 | 1.0 | 1.2 | 1.5 | 2.0 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | 6.3 |
I/A | 0 | 0.05 | 0.08 | 0.10 | 0.12 | 0.14 | 0.16 | 0.18 | 0.20 | 0.23 | 0.25 | 0.27 | 0.27 |
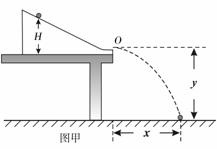
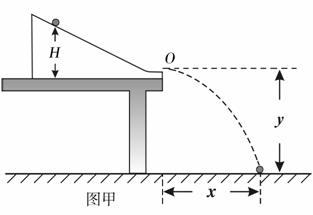
某同学利用如图所示的装置验证动能定理。固定并调整斜槽,使它的末端O点的切线水平,在水平地面上依次铺放好木板、白纸、复写纸。将小球从不同的标记点由静止释放,记录小球到达斜槽底端时下落的高度H,并根据落点位置测量出小球平抛的水平位移x。
改变小球在斜槽上的释放位置,进行多次测量,记录数据如下:
| 高度 H(h为单位长度) | h | 2h | 3h | 4h | 5h | 6h | 7h | 8h | 9h |
| 水平位移 x/cm | 5.5 | 9.1 | 11.7 | 14.2 | 15.9 | 17.6 | 19.0 | 20.6 | 21.7 |
(1)已知斜槽倾角为θ,小球与斜槽之间的动摩擦因数为μ,斜槽底端离地的高度为y,不计小球与水平槽之间的摩擦,小球从斜槽上滑下的过程中,动能定理若成立应满足的关系式是
;
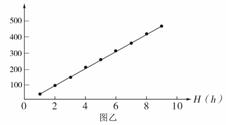
(2)以H为横坐标,以 为纵坐标,在坐标纸上描点作图,如图乙所示;
(3)由第(1)、(2)问,可以得出结论:
;
(4)受该实验方案的启发,某同学改用图乙的装置实验。他将木板竖直放置在斜槽末端的前方某一位置固定,仍将小球从不同的标记点由静止释放,记录小球到达斜槽底端时下落的高度H,并测量小球击中木板时平抛下落的高度d,他以H为横坐标,以 为纵坐标,描点作图,使之仍为一条倾斜的直线,也达到了同样的目的。

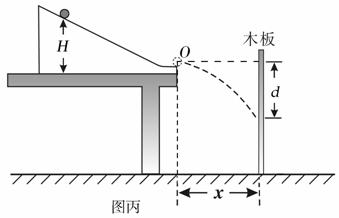
某同学利用如图所示的装置验
证动能定理。该装置由斜面和很短一段水平部分组成,固定并调整斜槽,使它的末端O点的切线水平,在水平地面上依次铺放好木板、白纸、复写纸。将小球从不同的标记点由静止释放,记录小球到达斜槽底端时下落的高度H,并根据落点位置测量出小球平抛的水平位移x。
改变小球在斜槽上的释放位置,进行多次测量,记录数据如下:
| 高度H(h为单位长度) | h | 2h | 3h | 4h | 5h | 6h | 7h | 8h | 9h |
| 水平位移 x/cm | 5.5 | 9.1 | 11.7 | 14.2 | 15.9 | 17.6 | 19.0 | 20.6 | 21.7 |
①已知斜槽倾角为θ,小球与斜槽之间的动摩擦因数为μ,斜槽底端离地的高度为y。小球从斜槽上滑下的过程中,动能定理若成立应满足的关系式是
(利用给定和测得的物理量)
②以H为横坐标,以 为纵坐标,在坐标纸上描点作图,如图乙所示。图线不过坐标原点的原因是 。