题目内容
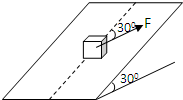 一个重为600N的物体放在倾角为30°的斜面上,物体与斜面间的摩擦因数μ=
一个重为600N的物体放在倾角为30°的斜面上,物体与斜面间的摩擦因数μ=| 1 | 3 |
(1)摩擦力的最小值是多少?
(2)力F的取值范围是多少?
分析:物体在斜面上静止,受力平衡,分析受力情况,将重力分解,作出物体在平行于斜面上的受力示意图.根据平衡条件求出物体所受的滑动摩擦力和支持力,再求解动摩擦因数.
解答:解:(1)物体受重力mg、支持力N、摩擦力f和拉力F注意而静止,在平行于斜面方向上有:重力的分力、拉力和摩擦力组成矢量三角形,当摩擦力垂直于拉力方向时,摩擦力由最小值fmin=mgsin230°=600×
=150N
(2)将物体的重力分解为垂直于斜面和平行于斜面两个方向的分力,在垂直于斜面的方向上,物体受到的支持力与重力垂直斜面的分力平衡.则
支持力FN=mgcosθ=600×
=300
N.
在斜面内,物体所受的拉力F、摩擦力Ff与重力的平行斜面的分力mgsinθ=300N平衡,
由物体的平衡条件得:滑动摩擦力Ff=μFN=100
N
由余弦定理可知:Ff=
,
解得F1=100
,F2=200
所以100
≤F≤200
N
答:(1)摩擦力的最小值是150N
(2)力F的取值范围是100
≤F≤200
N.
| 1 |
| 4 |
(2)将物体的重力分解为垂直于斜面和平行于斜面两个方向的分力,在垂直于斜面的方向上,物体受到的支持力与重力垂直斜面的分力平衡.则
支持力FN=mgcosθ=600×
| ||
| 2 |
| 3 |
在斜面内,物体所受的拉力F、摩擦力Ff与重力的平行斜面的分力mgsinθ=300N平衡,
由物体的平衡条件得:滑动摩擦力Ff=μFN=100
| 3 |
由余弦定理可知:Ff=
| (mgsin30°)2+F2-2mgsin30°F |
解得F1=100
| 3 |
| 3 |
所以100
| 3N |
| 3 |
答:(1)摩擦力的最小值是150N
(2)力F的取值范围是100
| 3N |
| 3 |
点评:本题物体受力分布在立体空间,分成垂直于斜面和平行于斜面两平面内研究,任何一个平面内物体的合力都为零.

练习册系列答案
相关题目
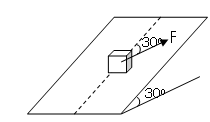
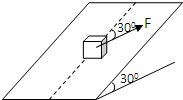 一个重为600N的物体放在倾角为30°的斜面上,物体与斜面间的摩擦因数
一个重为600N的物体放在倾角为30°的斜面上,物体与斜面间的摩擦因数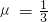 ,今用一个与图中虚线(虚线即为重力平行于斜面的向下的分力所在的直线)成30°平行于斜面的力F作用于物体上,如下图所示,使物体在斜面上始终保持静止状态,求
,今用一个与图中虚线(虚线即为重力平行于斜面的向下的分力所在的直线)成30°平行于斜面的力F作用于物体上,如下图所示,使物体在斜面上始终保持静止状态,求