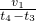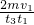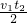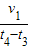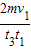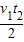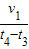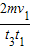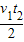题目内容
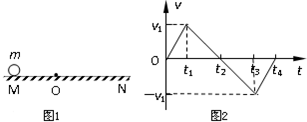
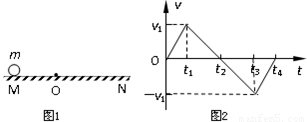
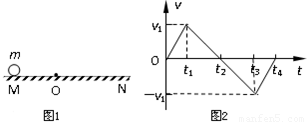
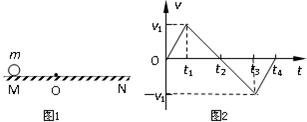 如图1所示,O为水平直线MN上的一点,质量为m的小球在O点的左方时受到水平恒力F1作用,运动到O点的右方时,同时还受到水平恒力F2的作用,设质点从图示位置由静止开始运动,其v-t图象如图2所示,由图可知( )
如图1所示,O为水平直线MN上的一点,质量为m的小球在O点的左方时受到水平恒力F1作用,运动到O点的右方时,同时还受到水平恒力F2的作用,设质点从图示位置由静止开始运动,其v-t图象如图2所示,由图可知( )分析:由v-t图可知物体的速度随时间变化的规律,并能求出物体各段时间内的加速度;根据物体的受力情况则可得出两力的大小关系;
解答:解:A、在0-t1时间内,小球在0的左方向向右做匀加速运动;在t1-t2时间内小球在0的右方向右做匀减速直线运动,在t2-t3时间内小球在0的右方向左做匀加速直线运动,根据运动过程的对称性得知,小球在0的右方运动的时间为t3-t1.故A错误;
B、图中0-t1与t3-t4两段时间内小球在0的左方运动,根据图线的斜率等于加速度得:物体在0的左方加速度为a=
=
=
=
,故B正确;
C、在t1-t3时间内,小球的加速度大小为a′=
=
,根据牛顿第二定律得:F2-F1=ma′,得到F2=F1+ma′=F1+
,故C错误;
D、小球在t=0到t=t4这段时间内在t2时刻离M点最远,最远距离为S=
,故D正确.
故选BD
B、图中0-t1与t3-t4两段时间内小球在0的左方运动,根据图线的斜率等于加速度得:物体在0的左方加速度为a=
| △v |
| △t |
| v1-0 |
| t4-t3 |
| △v |
| △t |
| v1 |
| t4-t3 |
C、在t1-t3时间内,小球的加速度大小为a′=
| v1-(-v1) |
| t3-t1 |
| 2v1 |
| t3-t1 |
| 2v1 |
| t3-t1 |
D、小球在t=0到t=t4这段时间内在t2时刻离M点最远,最远距离为S=
| v1t2 |
| 2 |
故选BD
点评:本题结合图象与牛顿运动定律,应通过图象得出物体的运动情况,再由牛顿第二定律即可求得受力情况.

练习册系列答案
相关题目
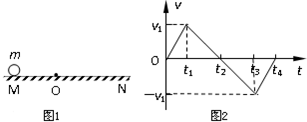 如图1所示,O为水平直线MN上的一点,质量为m的小球在O点的左方时受到水平恒力F1作用,运动到O点的右方时,同时还受到水平恒力F2的作用,设质点从图示位置由静止开始运动,其v-t图象如图2所示,由图可知
如图1所示,O为水平直线MN上的一点,质量为m的小球在O点的左方时受到水平恒力F1作用,运动到O点的右方时,同时还受到水平恒力F2的作用,设质点从图示位置由静止开始运动,其v-t图象如图2所示,由图可知