题目内容
 如图所示,木块m放在木板AB上,开始θ=0,现在木板A端 用一个竖直向上的力F使木板绕B端逆时针缓慢转动(B端不滑动).在m 相对AB保持静止的过程中
如图所示,木块m放在木板AB上,开始θ=0,现在木板A端 用一个竖直向上的力F使木板绕B端逆时针缓慢转动(B端不滑动).在m 相对AB保持静止的过程中
- A.木块m对木板AB的作用力逐渐减小
- B.木块m受到的静摩擦力随θ呈线性增大
- C.竖直向上的拉力F保持不变
- D.拉力F的力矩先逐渐增大再逐渐减小
C
分析:对m受力分析,受到重力、支持力和静摩擦力,根据共点力平衡条件列式求解;再对整体运用力矩平衡条件分析.
解答:A、木块m受重力、支持力和静摩擦力,其中支持力和静摩擦力都是木板对滑块的力,根据三力平衡条件,支持力和静摩擦力一定等于重力,根据牛顿第三定律,木块对木板的作用力也等于木板的重力,故A错误;
B、对m受力分析,受到重力、支持力和静摩擦力,如图
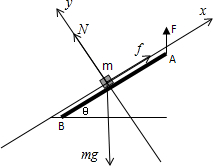
根据共点力平衡条件,有
f-mgsinθ=0
N-mgcosθ=0
解得
f=mgsinθ
即静摩擦力随着θ的增大而增大,但不是线性关系,故B错误;
C、对木块和木板整体而言,总重力要使板顺时针转动,拉力要使半逆时针转动,根据力矩平衡条件,有
F?Lcosθ=Mg cosθ+mglcosθ
cosθ+mglcosθ
其中:L为板长,l为木块与支持点的距离
解得:
F= Mg+
Mg+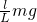 ,与角度θ无关,故C正确;
,与角度θ无关,故C正确;
D、拉力F的力矩为F?Lcosθ,故越来越小,故D错误;
故选C.
点评:本题关键对m受力分析,根据共点力平衡条件列式分析;在对M与m整体运用力矩平衡条件列式分析.
分析:对m受力分析,受到重力、支持力和静摩擦力,根据共点力平衡条件列式求解;再对整体运用力矩平衡条件分析.
解答:A、木块m受重力、支持力和静摩擦力,其中支持力和静摩擦力都是木板对滑块的力,根据三力平衡条件,支持力和静摩擦力一定等于重力,根据牛顿第三定律,木块对木板的作用力也等于木板的重力,故A错误;
B、对m受力分析,受到重力、支持力和静摩擦力,如图

根据共点力平衡条件,有
f-mgsinθ=0
N-mgcosθ=0
解得
f=mgsinθ
即静摩擦力随着θ的增大而增大,但不是线性关系,故B错误;
C、对木块和木板整体而言,总重力要使板顺时针转动,拉力要使半逆时针转动,根据力矩平衡条件,有
F?Lcosθ=Mg
 cosθ+mglcosθ
cosθ+mglcosθ其中:L为板长,l为木块与支持点的距离
解得:
F=
 Mg+
Mg+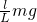 ,与角度θ无关,故C正确;
,与角度θ无关,故C正确;D、拉力F的力矩为F?Lcosθ,故越来越小,故D错误;
故选C.
点评:本题关键对m受力分析,根据共点力平衡条件列式分析;在对M与m整体运用力矩平衡条件列式分析.

练习册系列答案
相关题目
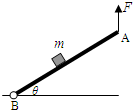 (2013?长宁区一模)如图所示,木块m放在薄板AB上(B端光滑铰链连接),开始θ=0,现在A端用一个竖直向上的力F使板绕B端逆时针缓慢转动,在m相对AB保持静止的过程中( )
(2013?长宁区一模)如图所示,木块m放在薄板AB上(B端光滑铰链连接),开始θ=0,现在A端用一个竖直向上的力F使板绕B端逆时针缓慢转动,在m相对AB保持静止的过程中( )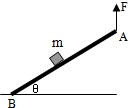 如图所示,木块m放在木板AB上,在木板的A端用一个竖直向上的力F使木板绕B端逆时针缓慢转动(B端不滑动).在此过程中,m与AB保持相对静止,则( )
如图所示,木块m放在木板AB上,在木板的A端用一个竖直向上的力F使木板绕B端逆时针缓慢转动(B端不滑动).在此过程中,m与AB保持相对静止,则( ) (2011?长宁区一模)如图所示,木块m放在木板AB上,开始θ=0,现在木板A端 用一个竖直向上的力F使木板绕B端逆时针缓慢转动(B端不滑动).在m 相对AB保持静止的过程中( )
(2011?长宁区一模)如图所示,木块m放在木板AB上,开始θ=0,现在木板A端 用一个竖直向上的力F使木板绕B端逆时针缓慢转动(B端不滑动).在m 相对AB保持静止的过程中( ) 如图所示,木块m放在木板AB上,在木板的A端用一个竖直向上的力F使木板绕固定支点B逆时针缓慢转动.在此过程中,m与AB保持相对静止,则 ( )
如图所示,木块m放在木板AB上,在木板的A端用一个竖直向上的力F使木板绕固定支点B逆时针缓慢转动.在此过程中,m与AB保持相对静止,则 ( )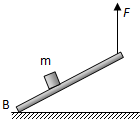 如图所示,木块m放在木板AB上,在木板的A端用一个竖直向上的力F使木板绕固定支点B逆时针缓慢转动.在此过程中,m与AB保持相对静止,则在m下滑之前( )
如图所示,木块m放在木板AB上,在木板的A端用一个竖直向上的力F使木板绕固定支点B逆时针缓慢转动.在此过程中,m与AB保持相对静止,则在m下滑之前( )