��Ŀ����
ij����ʵ��С������ʵ�����ṩ�����IJ���һ���߹���������֮�����˿�ij��ȣ���ѡ�õ��������£�
A���������߹��������� �����������߹ܵĽ���˿�ĵ�����Ϊ�ѣ���ֵΪ��ʮŷ��
�����������߹ܵĽ���˿�ĵ�����Ϊ�ѣ���ֵΪ��ʮŷ��
B��������A1������Ϊ10mA������r1=40����
C��������A2������Ϊ500��A������r2=750����
D����ѹ��V������Ϊ10V������Ϊ10k����
E����ֵ����R1����ֵΪ100����
F������������R2������ֵԼΪ10����
G����ԴE���綯��ԼΪ1.5V��������Բ��ƣ�
H������һ�����������ɣ�
��1���ö��õ���ֲ����˿�ĵ��裬ѡ���ʡ���1���͡���10��������ȷ������������õ������ʾ����ͼ�������˿�ĵ���ԼΪ ����
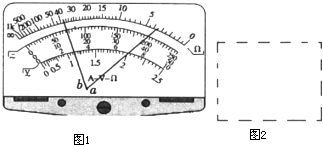
��2��Ϊ�˾�����ȷ�ز�����Ҫ������ָ��ƫת����Ҫ�ﵽ���̶ȵ�
���������һ���ʺϵĵ�·��������Ƶĵ�·���ڵ�����ͼ2���У��������������ĵĴ��ţ�
��3����֪����˿��ֱ��ΪD��Ҫ�������������� ������֪���Ͳ�����ķ��ű�ʾ����˿�ij���L����L= ��
A���������߹���������
 �����������߹ܵĽ���˿�ĵ�����Ϊ�ѣ���ֵΪ��ʮŷ��
�����������߹ܵĽ���˿�ĵ�����Ϊ�ѣ���ֵΪ��ʮŷ��B��������A1������Ϊ10mA������r1=40����
C��������A2������Ϊ500��A������r2=750����
D����ѹ��V������Ϊ10V������Ϊ10k����
E����ֵ����R1����ֵΪ100����
F������������R2������ֵԼΪ10����
G����ԴE���綯��ԼΪ1.5V��������Բ��ƣ�
H������һ�����������ɣ�
��1���ö��õ���ֲ����˿�ĵ��裬ѡ���ʡ���1���͡���10��������ȷ������������õ������ʾ����ͼ�������˿�ĵ���ԼΪ

��2��Ϊ�˾�����ȷ�ز�����Ҫ������ָ��ƫת����Ҫ�ﵽ���̶ȵ�
| 1 | 3 |
��3����֪����˿��ֱ��ΪD��Ҫ��������������
����������Ĺؼ������Դ�綯��С�ڵ�ѹ�����̵�
�����Բ���ʹ�õ�ѹ����ֻ��ʹ��������������Ȼ���������������ƫ��������ƫ��ѹ��Ĺ�ϵ���������ֿ��ܵĵ�·ͼ��������⣮
| 1 |
| 3 |
����⣺��1������ŷķ��ָ��ָ��ŷķ����ֵ���踽��ʱ������������Ӧ����1���ʶ���������ΪR=1��38��=38����
��2�����ڵ�Դ�綯��Ϊ1.5V��С�ڵ�ѹ������
�����Բ���ʹ�õ�ѹ��V��������ѹ������������������ƫ��ѹ�ֱ�ΪU1=I1r1=0.4V��U2=I2r2=0.375V���ɽ���������������A2����Ȼ������A1 ���������·һͼ��ʾ�������������A2����ƫ����С�� A1 ����ƫ�������ɽ��������������� A2��������A1 ���������·ͼ����ʾ���������ڻ�����������������ԶС�ڴ�����裬���Ա�����Ӧ�÷�ѹʽ�ӷ��������ֵ�·ͼѡ����һ�ּ��ɣ�
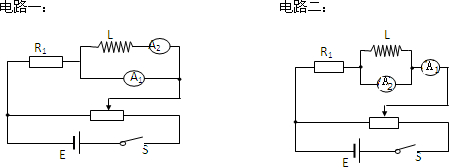
��3�����ǵ�·һ����I2��R+r2��=I1r1����R=
��������ã�L=
��
���õ�·������I1=I2+
����R=
��������ã�L=
��
�ʴ�Ϊ����1��38����2����ͼ��ʾ����3��ͨ������A1�ĵ���I1��ͨ��������A2�ĵ���I2��
��
��
��2�����ڵ�Դ�綯��Ϊ1.5V��С�ڵ�ѹ������
| 1 |
| 3 |

��3�����ǵ�·һ����I2��R+r2��=I1r1����R=
| ��L | ||
|
| ��D2I2r2 |
| 4��(I1-I2) |
���õ�·������I1=I2+
| I2r2 |
| R |
| ��L | ||
|
| ��D2I2r2 |
| 4��(I1-I2) |
�ʴ�Ϊ����1��38����2����ͼ��ʾ����3��ͨ������A1�ĵ���I1��ͨ��������A2�ĵ���I2��
| ��D2I2r2 |
| 4��(I1-I2) |
| ��D2I2r2 |
| 4��(I1-I2) |
��������������ķ������˷������⣬���С�������������������������ϣ���������������������ѹ����ϣ��ȣ�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ������ѧ��һij����ѧϰС���ڼ��ij��綯�����ܵ�ʵ���У��õ綯���ɾ�ֹ��ʼ��ƽֱ��·��ʻ������������ò�ͬʱ�̵綯����ǣ����F���Ӧ���ٶ�v�������
������ѧ��һij����ѧϰС���ڼ��ij��綯�����ܵ�ʵ���У��õ綯���ɾ�ֹ��ʼ��ƽֱ��·��ʻ������������ò�ͬʱ�̵綯����ǣ����F���Ӧ���ٶ�v������� ͼ����ͼ��ʾ��ͼ��AB��BD��Ϊֱ�ߣ�C��Ϊʵ�������ߵķֽ�㣩.����綯����ʻ�����ܵ������㶨������ͼ���֪��
ͼ����ͼ��ʾ��ͼ��AB��BD��Ϊֱ�ߣ�C��Ϊʵ�������ߵķֽ�㣩.����綯����ʻ�����ܵ������㶨������ͼ���֪��
 ͼ����ͼ��ʾ��ͼ��AB��BD��Ϊֱ�ߣ�C��Ϊʵ�������ߵķֽ�㣩������綯����ʻ�����ܵ������㶨������ͼ���֪��
ͼ����ͼ��ʾ��ͼ��AB��BD��Ϊֱ�ߣ�C��Ϊʵ�������ߵķֽ�㣩������綯����ʻ�����ܵ������㶨������ͼ���֪��
 ͼ����ͼ��ʾ��ͼ��AB��BD��Ϊֱ�ߣ�C��Ϊʵ�������ߵķֽ�㣩.����綯����ʻ�����ܵ������㶨������ͼ���֪��
ͼ����ͼ��ʾ��ͼ��AB��BD��Ϊֱ�ߣ�C��Ϊʵ�������ߵķֽ�㣩.����綯����ʻ�����ܵ������㶨������ͼ���֪��