题目内容
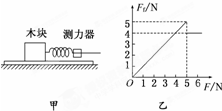在研究摩擦力特点的实验中，将木块放在水平长木板上，如图甲所示，用力沿水平方向拉木块，拉力从0开始逐渐增大．用特殊的测力仪器测出拉力和摩擦力，并绘制出摩擦力Ff随拉力F变化的图象，如图乙所示．已知木块质量为2kg，取g=10m/s2．（1）求木块与长木板间的动摩擦因数；
（2）若将实验中的长木板与水平方向成37°角放置，将木块置于其上，木块在平行于木板的恒力F作用下，从静止开始向上做匀变速直线运动，沿斜面向上运动4m，速度达到4m/s，求此拉力F的大小．（sin37°=0.6，cos37°=0.8）
分析：（1）通过图象得出最大静摩擦力和滑动摩擦力的大小，根据Ff=μFN求出动摩擦因数的大小．
（2）根据物体的运动求得加速度，再对物体进行受力分析，由牛顿第二定律求解即可．
（2）根据物体的运动求得加速度，再对物体进行受力分析，由牛顿第二定律求解即可．
解答：
解：由乙图象可知：Ff的最大值为5N，就是木块受到的最大静摩擦力，木块受到的滑动摩擦力大小为Ff=4N．
（1）设木块与木板间的动摩擦因数为μ，由图乙知木块受到的滑动摩擦力Ff=μFN=μmg=4 N，解得μ=0.2．
（2）设木块在斜面上的加速度为a，由v2=2ax解得a=2 m/s2
对木块受力分析如图所示，建立直角坐标系，由牛顿第二定律得
F-mgsinθ-Ff′=ma
FN′-mgcosθ=0
又F
=μF
所以可以解得F=19.2 N．
答：（1）木块与长木板间的动摩擦因数μ=0.2
（2）拉力F的大小为19.2 N．
解：由乙图象可知：Ff的最大值为5N，就是木块受到的最大静摩擦力，木块受到的滑动摩擦力大小为Ff=4N．（1）设木块与木板间的动摩擦因数为μ，由图乙知木块受到的滑动摩擦力Ff=μFN=μmg=4 N，解得μ=0.2．
（2）设木块在斜面上的加速度为a，由v2=2ax解得a=2 m/s2
对木块受力分析如图所示，建立直角坐标系，由牛顿第二定律得
F-mgsinθ-Ff′=ma
FN′-mgcosθ=0
又F
′ f |
′ N |
所以可以解得F=19.2 N．
答：（1）木块与长木板间的动摩擦因数μ=0.2
（2）拉力F的大小为19.2 N．
点评：解决本题的关键知道最大静摩擦力和滑动摩擦力的区别，掌握滑动摩擦力的大小公式Ff=μFN．利用牛顿第二定律根据运动求物体的作用力．
练习册系列答案
相关题目
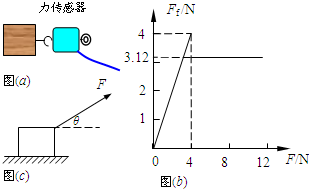（2010?上海模拟）在研究摩擦力特点的实验中，将木块放在水平长木板上，如图a所示，用力沿水平方向拉木块，拉力从0开始逐渐增大．分别用力传感器采集拉力和木块所受到的摩擦力，并用计算机绘制出摩擦力Ff随拉力F的变化图象，如图b所示．已知木块质量为0.78kg．取重力加速度g=10m/s2，sin37°=0.60，cos37°=0.80．
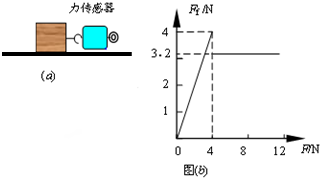在研究摩擦力特点的实验中，将木块放在水平长木板上，如图a所示，用力沿水平方向拉木块，拉力从0开始逐渐增大．分别用力传感器采集拉力和木块所受到的摩擦力，并用计算机绘制出摩擦力Ff随拉力F的变化图象，如图b所示．已知木块质量为0.8kg．取重力加速度g=10m/s2．则木块与长木板间的动摩擦因数为（ ）
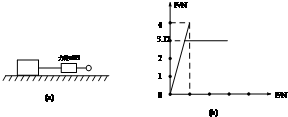在研究摩擦力特点的实验中，将木块放在水平长木板上如图（a）所示，用力沿水平方向拉木块，拉力从0开始逐渐增大，分别用力传感器采集拉力和木块所受到的摩擦力，并用计算机绘制出摩擦力Ff随拉力F的变化图象如图（b）所示．已知木块的质量为0.78kg，取重力加速度g=10m/s2求：
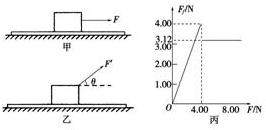（2011?德清县模拟）在研究摩擦力特点的实验中，将木块放在足够长的静止水平木板上．如图甲所示，用力沿水平方向拉木块，使拉力F从0开始逐渐增大．经实验绘制出摩擦力Ff随拉力F的变化图象如图丙所示．已知木块质量为0.78kg．