题目内容
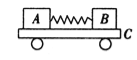
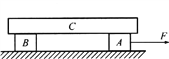
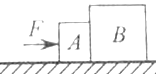
【题目】如图所示，质量分别为mA=l kg、mB=3 kg的物块A、B置于足够长的水平面上， 在水平推力F作用下一起由静止开始向右做匀加速运动，加速度a=2m/s2.已知A、B与水平面间的动摩擦因数分别为μA=0.2、μB= 0.1,取g=10 m/s2.求：
(1)物块A对物块B的作用力；
(2)水平推力F的大小；
(3)某时刻A、B的速度为v=2m/s,此时撤去水平推力F，求撤去推力后物块A、B间的最大距离
【答案】(1) F′= 9N ，方向水平向右 (2) 13 N (3) 1 m
【解析】
（1）以物块B为研究对象，根据牛顿第二定律求解物块A对物块B的作用力大小；
（2）整体由牛顿第二定律求解水平推力F的大小；
（3）根据牛顿第二定律求出二者减速运动的加速度大小，根据位移速度关系求解运动的位移，最后求出物块A、B间的最大距离;
（1）设物块A对物块B的作用力大小为
，以物块B为研究对象，则：
，代入数据解得：
,方向水平向右;
（2）设物块A、B一起做匀加速运动的加速度为a，则由牛顿第二定律得：
，代入数据解得：
方向与加速度的方向相同，即方向水平向右;
（3）撤去水平力F后，物块A、B都做匀减速运动，设它们的加速度分别为
，则根据牛顿第二定律可得：
，
，
代入数据解得：
，
，
物块A运动的位移为：
，
物块B运动的位移为：
，
物块A、B间的最大距离为：
。
练习册系列答案
名校课堂系列答案
相关题目
