题目内容
(09年英雄山中学期末)(14分)如图所示,一带电粒子以某一速度在竖直平面内做直线运动,经过一段时间后进入一垂直于纸面向里、磁感应强度为B的匀强磁场区域(图中未画出磁场区域),粒子飞出磁场后垂直电场方向进入宽为L的匀强电场。电场强度大小为E,方向垂直向上。当粒子穿出电场时速度方向改变了45°角。已知带电粒子的质量为m,电量为q,重力不计。粒子进入磁场前的速度如图与水平方向成θ=60°角。试解答:
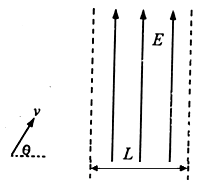
(1)粒子带正电还是负电?
(2)带电粒子在磁场中运动时速度多大?
(3)若磁场区域为圆形,则最小的圆形磁场区域的半径为多大?
解析:
(1)根据粒子在磁场中偏转的情况和左手定则可知,粒子带负电。 (3分)
(2)由于洛仑兹力对粒子不做功,故粒子以原来的速率进入电场中,设带电粒子进入电场的初速度为v0,在电场中偏转时做类平抛运动,由题意知粒子离开电场时的末速度与初速度夹角为45°,将末速度分解为平行于电场方向和垂直于电场方向的两个分速度vx和vy,由几何关系知

vx=vy= v0 (2分)
vy=at (1分)
qE=ma (1分)
L=v0t (1分)
解得: ![]() (2分)
(2分)
(3)如图所示,带电粒子在磁场中所受洛仑兹力作为向心力,设在磁场中做圆周运动的半径为R,圆形磁场区域的半径为r,则:
![]() (1分)
(1分)
![]() (1分)
(1分)
由几何知识可得:![]() (2分)
(2分)