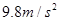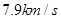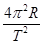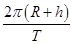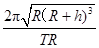题目内容
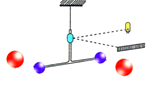
在发射地球同步卫星的过程中，卫星首先进入椭圆轨道Ⅰ，然后在Q点通过改变卫星速度，让卫星进入地球同步轨道Ⅱ。若卫星的发射速度为v0，第一宇宙速度为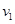
，在同步轨道Ⅱ上的运行速度为
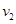，则
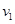，在同步轨道Ⅱ上的运行速度为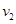，则| A．v0＞＞ |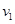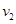
| B．若卫星的发射速度为2v0，卫星最终围绕地球运行的轨道半径将变大。 |
| C．在轨道Ⅰ上，卫星在P点的速度等于在Q点的速度 |
| D．卫星在Q点通过加速实现由轨道Ⅰ进入轨道Ⅱ |
AD
试题分析：7.9km/s即第一宇宙速度是发射卫星的最小速度，也是最大的圆周运动的环绕速度，而同步卫星的轨道半径要大于近地卫星的轨道半径，根据
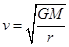可以发现，同步卫星运行的线速度一定小于第一宇宙速度，故v0＞v1＞v2，所以A正确；若卫星的发射速度为2v0，即大于11.2km/s，将脱离地球，所以B错误；卫星首先进入椭圆轨道Ⅰ，在轨道Ⅰ上，由P点向Q点运动，万有引力做负功，动能减小，所以P点的速度大于Q点的速度，故C错误；从椭圆轨道Ⅰ到同步轨道Ⅱ，卫星在Q点是做逐渐远离圆心的运动，要实现这个运动必须卫星所需向心力大于万有引力，所以应给卫星加速，增加所需的向心力．所以在轨道Ⅱ上Q点的速度大于轨道上Ⅰ经过Q点的速度．故D正确
练习册系列答案
相关题目
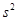，月球半径为R，引力常量G．求：
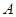变轨进入绕月飞行圆轨道；已知“嫦娥一号”绕月飞行的椭圆轨道远月点
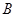距月球表面高度为
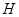；又已知“嫦娥一号”绕月圆轨道飞行时，距月球表面的高度为
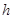，飞行周期为
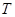，月球的半径为
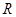，万有引力常量为
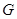；再后，假设宇航長在飞船上，操控飞船在月球表面附近竖直平面内俯冲，在最低点附近作半径为
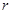的圆周运动，宇航员质量是
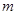，飞船经过最低点时的速度是
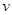．求：
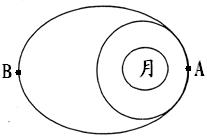
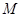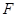是多大？
是多大？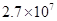
倍，地球绕太阳运行的轨道半径约为月球绕地球运行的轨道半径的400倍。关于太阳和月球对地球上相同质量海水的引力，以下说法正确的是
