题目内容
如图，一个滑板运动员，滑板和人的总质量为50kg，以某一初速度从一个斜坡底端滑上斜坡，当速度减小为零时，又从斜坡上下滑至底端，已知斜坡的倾角为30°，运动员上滑的时间是2s，设人及滑板受到的阻力（包括摩擦力和空气阻力）的大小恒为50N，g取10m/s2．求：
（1）滑板从斜坡底端滑上时的初速度大小；
（2）运动员匀加速下滑到底端时所用的时间．
解：（1）设运动员向上滑行时的加速度为a1，设初速度的方向为正方向，根据牛顿第二定律有：
-（mgsinθ+f）=ma1
代入数据得：a1=-6m/s2
根据运动学的规律有：0=v0+a1t1
代入数据得：v0=12m/s．
（2）设运动员下滑时的加速度大小为a2，根据牛顿第二定律有：
mgsinθ-f=ma2
代入数据得：a2=4m/s2
运动员上滑的位移为：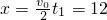
m
下滑的与上滑的距离相同，设运动员匀加速下滑到底端时所用的时间t2．
则有：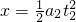
代入数据得：t2=
s
答：（1）滑板从斜坡底端滑上时的初速度大小为12m/s．
（2）运动员匀加速下滑到底端时所用的时间为s．
分析：（1）根据牛顿第二定律求出运动员上滑的加速度，根据上滑的时间，运用速度时间公式求出滑板从斜坡底端滑上时的初速度大小．
（2）根据平均速度公式求出运动员上滑的位移，从而得知下滑的位移，根据牛顿第二定律求出下滑的加速度，根据位移时间公式求出运动员匀加速下滑到底端时所用的时间．
点评：解决本题的关键能够正确地对运动员进行受力分析，结合牛顿第二定律和运动学公式进行求解．
-（mgsinθ+f）=ma1
代入数据得：a1=-6m/s2
根据运动学的规律有：0=v0+a1t1
代入数据得：v0=12m/s．
（2）设运动员下滑时的加速度大小为a2，根据牛顿第二定律有：
mgsinθ-f=ma2
代入数据得：a2=4m/s2
运动员上滑的位移为：
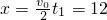m下滑的与上滑的距离相同，设运动员匀加速下滑到底端时所用的时间t2．
则有：
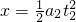
代入数据得：t2=
s答：（1）滑板从斜坡底端滑上时的初速度大小为12m/s．
（2）运动员匀加速下滑到底端时所用的时间为
s．分析：（1）根据牛顿第二定律求出运动员上滑的加速度，根据上滑的时间，运用速度时间公式求出滑板从斜坡底端滑上时的初速度大小．
（2）根据平均速度公式求出运动员上滑的位移，从而得知下滑的位移，根据牛顿第二定律求出下滑的加速度，根据位移时间公式求出运动员匀加速下滑到底端时所用的时间．
点评：解决本题的关键能够正确地对运动员进行受力分析，结合牛顿第二定律和运动学公式进行求解．
练习册系列答案
阅读快车系列答案
相关题目
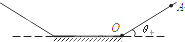滑雪运动常在两个斜面和一个平面的组合场地中进行，我们把它简化为理想情景如图所示．假定运动员和滑板的总质量为m=60kg，从O点以初速度v0=2m/s冲上倾角为θ=37°的斜面，则经过t=5/24s时间第一次冲到斜面的最高
如图，一个滑板运动员，滑板和人的总质量为50kg，以某一初速度从一个斜坡底端滑上斜坡，当速度减小为零时，又从斜坡上下滑至底端，已知斜坡的倾角为30°，运动员上滑的时间是2s，设人及滑板受到的阻力（包括摩擦力和空气阻力）的大小恒为50N，g取10m/s2．求：
