题目内容
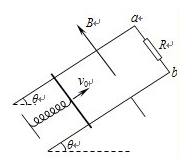
(20分) 如图所示,在空间有两个磁感强度均为B的匀强磁场区域,上一个区域边界AA¢与BB¢的间距为H,方向垂直纸面向里,CC¢与BB¢的间距为h,CC¢下方是另一个磁场区域,方向垂直纸面向外。现有一质量为m,边长为L(0.5H < L < H;h < L)的正方形线框由AA¢上方某处竖直自由落下,线框总电阻为R,已知当线框cd边到达AA¢和BB¢正中间时加速度大小为g。
(1) 判断线框穿入磁场至加速度大小为g的过程中是做加速还是减速运动,并说明判断依据。
(2) 求cd到达AA¢和BB¢正中间时线框速度。
(3) 若cd边进 入CC¢前的瞬间线框的加速度大小变为0.8g,则线框进入CC¢后的瞬间线框的加速度多大?
(4) 求: cd边在AA¢和BB¢正中间位置到cd边刚穿进CC¢的过程中线框发热量。
(1)减速运动(2) (3)6.2g;(4)
(3)6.2g;(4)
解析试题分析:(1) 线框穿入磁场做减速运动.
因为安培力总是竖直向上的,若线框加速度向下,大小必小于g,因此线框大小为g的加速度方向必向上,所以线框穿入磁场过程做减速运动。
(2) BI1L-mg = ma1 (a1 ="g)" , ,解得:
,解得: 
(3) 线框cd边进入CC¢前瞬间的加速度大小为0.8g,此加速度方向也必向上.
设此时安培力为F,则 F-mg = ma2 (a2=0.8g)
cd边进入CC¢后瞬间,ab、cd都切割磁感线,电流瞬间增为原来2倍,且ab、cd都受向上安培力,安培力瞬间增为原来4倍.
此时有 4F-mg = ma3 ,解得:a3=6.2g
(4) F = BI2L, ,解得:
,解得:
线框发热量  =
=
考点:法拉第电磁感应定律;牛顿定律及能量守恒定律。

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
 N/C的匀强电场中,甲的质量为
N/C的匀强电场中,甲的质量为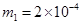 kg,带电荷量为
kg,带电荷量为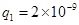 C,乙的质量为
C,乙的质量为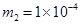 kg,带电荷量为
kg,带电荷量为 C。开始时细绳处于拉直状态。由静止释放两滑块,t=3s时细绳断裂,不计滑块间的库仑力。试求:
C。开始时细绳处于拉直状态。由静止释放两滑块,t=3s时细绳断裂,不计滑块间的库仑力。试求: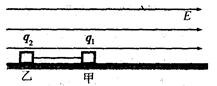
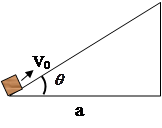


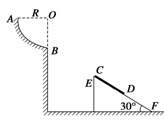
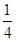 圆弧轨道,EF是一倾角为30°的足够长的光滑固定斜面,斜面上有一质量为0.1 kg的薄木板CD,开始时薄木板被锁定.一质量也为0.1 kg的物块(图中未画出)从A点由静止开始下滑,通过B点后水平抛出,经过一段时间后恰好以平行于薄木板的方向滑上薄木板,在物块滑上薄木板的同时薄木板解除锁定,下滑过程中某时刻物块和薄木板能达到共同速度.已知物块与薄木板间的动摩擦因数为μ=
圆弧轨道,EF是一倾角为30°的足够长的光滑固定斜面,斜面上有一质量为0.1 kg的薄木板CD,开始时薄木板被锁定.一质量也为0.1 kg的物块(图中未画出)从A点由静止开始下滑,通过B点后水平抛出,经过一段时间后恰好以平行于薄木板的方向滑上薄木板,在物块滑上薄木板的同时薄木板解除锁定,下滑过程中某时刻物块和薄木板能达到共同速度.已知物块与薄木板间的动摩擦因数为μ=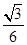 .(g=10 m/s2,结果可保留根号)求:
.(g=10 m/s2,结果可保留根号)求: