题目内容
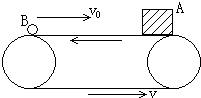
如图所示,足够长的水平传送带始终以大小为v=3m/s的速度逆时针传动,传送带上有一质量为M=2kg的小木盒A,A与传送带之间的动摩擦因数μ=0.3.开始时,A随同传送带共同向左运动,一光滑的质量为m=1kg的小球B自传送带左端出发,以一定的初速度在传送带上向右运动,小球与木盒相遇后,立即进入盒中与盒达到方向向右的共同速度v1=3m/s.(取g=10m/s2)求:
(1)木盒在传送带上相对滑动的距离为多少?
(2)为维持传送带始终匀速运动,带动传送带的电动机为此需多消耗的电能为多少?
(1)木盒在传送带上相对滑动的距离为多少?
(2)为维持传送带始终匀速运动,带动传送带的电动机为此需多消耗的电能为多少?

分析:(1)小球和盒子先向右做匀减速直线运动到零,然后向左做匀加速直线运动,直到速度达到传送带的速度,又一起做匀速直线运动,求出在这段时间内木盒的位移和传送带的位移,从而求出木盒在传送带上的相对位移.
(2)根据能量守恒得,电动机需多消耗的电能全部转化为摩擦产生的内能,根据Q=f△s求出摩擦产生的内能.
(2)根据能量守恒得,电动机需多消耗的电能全部转化为摩擦产生的内能,根据Q=f△s求出摩擦产生的内能.
解答:解:(1)设小球和小木盒一起做变速运动时的加速度为a,摩擦力为f,做变速运动的时间为t,由题可知,小球和木盒先相对地向右做匀减速运动,速度减到零,然后再向左做匀加速运动,直到速度为传送带速度为止.
F合=f=μ(M+m)g
a=
=μg=3m/s2
t=2×
=2s
在2s内木盒的位移为0,则木盒在传送带上滑过的距离等于这段时间传送带的对地位移大小.
即△s=vt=6m
故木盒在传送带上相对滑动的距离为6m.
(2)传送带上的物体动能和势能没有增加,所以电动机多消耗的电能为克服摩擦力做功产生的内能,即
E电=△Q=μ(m+M)△l=54J.
F合=f=μ(M+m)g
a=
| F合 |
| M+m |
t=2×
| v1 |
| a |
在2s内木盒的位移为0,则木盒在传送带上滑过的距离等于这段时间传送带的对地位移大小.
即△s=vt=6m
故木盒在传送带上相对滑动的距离为6m.
(2)传送带上的物体动能和势能没有增加,所以电动机多消耗的电能为克服摩擦力做功产生的内能,即
E电=△Q=μ(m+M)△l=54J.
点评:解决本题的关键知道木盒在传送带上先向右做匀减速直线运动到零,然后向左做匀加速直线运动,直到速度达到传送带的速度,又一起做匀速直线运动.以及知道电动机多消耗的电能为克服摩擦力做功产生的内能.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,足够长的水平直轨道MN上左端有一点C,过MN的竖直平面上有两点A、B,A点在C点的正上方,B点与A点在一条水平线上,不计轨道阻力和空气阻力,下面判断正确的是( )
如图所示,足够长的水平直轨道MN上左端有一点C,过MN的竖直平面上有两点A、B,A点在C点的正上方,B点与A点在一条水平线上,不计轨道阻力和空气阻力,下面判断正确的是( )