题目内容
16.已知质量为m的物体在质量为M的星球上的万有引力势能Ep=-$\frac{GMm}{r}$(以无穷远处势能为零,G为引力常量,r表示物体到该星球中心的距离).只要物体在星球表面具有足够大的速度,就可以脱离该星球的万有引力而飞离星球(即到达势能为零的地方).这个速度叫做第二宇宙速度.一旦第二宇宙速度的大小超过了光速,则该星球上的任何物体(包括光子)都无法摆脱该星球的引力.于是它就将与外界断绝了一切物质和信息的交流.从宇宙的其他部分看来,它就像是消失了一样,这就是所谓的“黑洞”.试分析一颗质量为M=2.0×1031kg的恒星,当它的半径为3×104m时就会成为一个“黑洞”?(计算时取引力常量G=7×10-11N•m2/kg2,(答案保留一位有效数字)分析 物体被发射出去后脱离星球的过程中只有引力做功,机械能守恒,由机械能守恒定律可以求出第二宇宙速度,当第二宇宙速度大于光速时,星球成为黑洞,根据题目所给数据求出恒星变为黑洞时的半径.
解答 解:设第二宇宙速度为v,由机械能守恒定律得:
$\frac{1}{2}$mv2-$\frac{GMm}{r}$=0,
解得:v=$\sqrt{\frac{2GM}{r}}$,
当v=c时,恒星成为黑洞,即:c=$\sqrt{\frac{2GM}{r}}$,
则:r=2$\frac{GM}{{c}^{2}}$=2×$\frac{7×1{0}^{-11}×2×1{0}^{31}}{(3×1{0}^{8})^{2}}$≈3×104m;
故答案为:3×104m.
点评 本题是一道信息给予题,认真审题,理解题意,根据题意获取所需信息是正确解题的关键,应用能量守恒定律可以解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.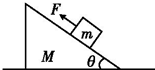 如图所示,质量为M的楔形物块静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.地面对楔形物块的支持力和摩擦力分别为( )
如图所示,质量为M的楔形物块静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.地面对楔形物块的支持力和摩擦力分别为( )
 如图所示,质量为M的楔形物块静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.地面对楔形物块的支持力和摩擦力分别为( )
如图所示,质量为M的楔形物块静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.地面对楔形物块的支持力和摩擦力分别为( )| A. | f=Fcosθ | B. | f=Fsinθ | C. | N=(M+m)g+Fsinθ | D. | N=(M+m)g-Fsinθ |
5.下列关于静电场的说法正确的是( )
| A. | 静电场中,电场强度大的点电势必定高 | |
| B. | 静电场中,电场强度为零的点电势必定为零 | |
| C. | 静电场中,在电势高的点点电荷的电势能必定高 | |
| D. | 无论是匀强电场还是点电荷形成的电场,电场强度与放在该处的试探电荷无关 |
 打印机是办公的常用工具,喷墨打印机是其中的一种.图是喷墨打印机的工作原理简化图.其中墨盒可以喷出半径约为10-5m的墨汁微滴,大量的墨汁微滴经过带电室时被带上负电荷,成为带电微粒.墨汁微滴所带电荷量的多少由计算机的输入信号按照文字的排列规律进行控制.带电后的微滴以一定的初速度进入由两块平行带电金属板形成的偏转电场中,微滴经过电场的作用发生偏转后打在纸面上,显示出字体.若某种喷墨打印机的偏转电场极板长度为l,两板间的距离为d,偏转电场极板的右端距纸面的距离为b,某个带电微滴的质量为m,沿两板间的中心线以初速度v0进入偏转电场.偏转电场两极板间电压为U.该微滴离开电场时的速度大小为v,不计微滴受到的重力和空气阻力影响,忽略电场边沿处场强的不均匀性.
打印机是办公的常用工具,喷墨打印机是其中的一种.图是喷墨打印机的工作原理简化图.其中墨盒可以喷出半径约为10-5m的墨汁微滴,大量的墨汁微滴经过带电室时被带上负电荷,成为带电微粒.墨汁微滴所带电荷量的多少由计算机的输入信号按照文字的排列规律进行控制.带电后的微滴以一定的初速度进入由两块平行带电金属板形成的偏转电场中,微滴经过电场的作用发生偏转后打在纸面上,显示出字体.若某种喷墨打印机的偏转电场极板长度为l,两板间的距离为d,偏转电场极板的右端距纸面的距离为b,某个带电微滴的质量为m,沿两板间的中心线以初速度v0进入偏转电场.偏转电场两极板间电压为U.该微滴离开电场时的速度大小为v,不计微滴受到的重力和空气阻力影响,忽略电场边沿处场强的不均匀性. P、Q是一条电场线上的两个点,一带正电的粒子仅在电场力作用下以一定的初速度从P点沿电场线运动到Q点,其v-t图象如图所示.则这电场的电场线分布可能是如图中的( )
P、Q是一条电场线上的两个点,一带正电的粒子仅在电场力作用下以一定的初速度从P点沿电场线运动到Q点,其v-t图象如图所示.则这电场的电场线分布可能是如图中的( )




 A、B是水平放置的平行板电容器,当A、B两板直接接到电源两极时,一电子从A板由静止飞到B板时的速度为v0.电源内阻r=1Ω,R1=4Ω,现若按图示连接,当开关S闭合时,电子从A板由静止飞到B板的过程中,通过两板的中点C的速度为$\frac{1}{2}$v0,当开关S断开时,电子从A板由静止飞向B板经C点时的速度为$\frac{\sqrt{3}}{3}$v0,求R2和R3的阻值.
A、B是水平放置的平行板电容器,当A、B两板直接接到电源两极时,一电子从A板由静止飞到B板时的速度为v0.电源内阻r=1Ω,R1=4Ω,现若按图示连接,当开关S闭合时,电子从A板由静止飞到B板的过程中,通过两板的中点C的速度为$\frac{1}{2}$v0,当开关S断开时,电子从A板由静止飞向B板经C点时的速度为$\frac{\sqrt{3}}{3}$v0,求R2和R3的阻值.