题目内容
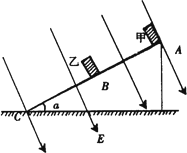
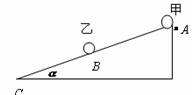
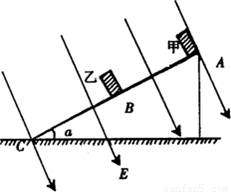
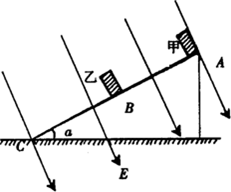 如图绝缘斜面AC的倾角α=37°,AB=BC=l,AB之间斜面光滑,BC之间斜面粗糙,在A、B两点分别放置质量均为m,带电量均为q的小滑块甲和乙,当所加匀强电场的方向垂直斜面向上时,两滑块均以相同的加速度沿斜面下滑.若保持电场强度大小不变,方向改为垂直斜面向下,再从A、B两点由静止释放滑块,滑块乙静止,甲加速下滑与乙碰撞,碰撞后甲和乙没有分开,为使它们不能到达C点,滑块与斜面间的动摩擦因数μ为多大?(两滑块均视为质点,g=10m/s2,sin37=0.6)
如图绝缘斜面AC的倾角α=37°,AB=BC=l,AB之间斜面光滑,BC之间斜面粗糙,在A、B两点分别放置质量均为m,带电量均为q的小滑块甲和乙,当所加匀强电场的方向垂直斜面向上时,两滑块均以相同的加速度沿斜面下滑.若保持电场强度大小不变,方向改为垂直斜面向下,再从A、B两点由静止释放滑块,滑块乙静止,甲加速下滑与乙碰撞,碰撞后甲和乙没有分开,为使它们不能到达C点,滑块与斜面间的动摩擦因数μ为多大?(两滑块均视为质点,g=10m/s2,sin37=0.6)分析:当所加电场方向垂直斜面向上时,两滑块均以相同的加速度沿斜面下滑,根据牛顿第二定律得出此时弹力为零.
从A到B,由运动学公式求出甲与乙碰撞前的速度,甲与乙碰撞,由动量守恒定律表示出碰撞后的速度.
甲与乙碰撞后,以两滑块为研究对象,由牛顿第二定律结合运动学公式求解.
从A到B,由运动学公式求出甲与乙碰撞前的速度,甲与乙碰撞,由动量守恒定律表示出碰撞后的速度.
甲与乙碰撞后,以两滑块为研究对象,由牛顿第二定律结合运动学公式求解.
解答:解:当所加电场方向垂直斜面向上时,两滑块均以相同的加速度沿斜面下滑,由于AB段光滑,滑块甲沿斜面下滑的加速度为g?sinα.
对于滑块乙应有沿斜面下滑的加速度g?sinα,
则:f=μFN=0,
而:FN+qE-mg?cosα?=0
故有:qE=mg?cosα
当所加电场方向垂直斜面向下时,滑块乙静止,
对甲有:mgsinα=ma1
从A到B,由运动学公式得:
=2a1l
甲与乙碰撞,由动量守恒定律,得:mv1=2mv
甲与乙碰撞后,以两滑块为研究对象,由牛顿第二定律,
得:μF′N-2mgsinα=(m+m)a2
即??μ(2Eq+2mgcosα)-2mgsinα=2ma2
从B到C由运动学公式,得:
=2a2l
联解得:μ=
≈0.47,
即要使甲、乙不能到C点,须有μ>0.47
答:为使它们不能到达C点,滑块与斜面间的动摩擦因数大于0.47.
对于滑块乙应有沿斜面下滑的加速度g?sinα,
则:f=μFN=0,
而:FN+qE-mg?cosα?=0
故有:qE=mg?cosα
当所加电场方向垂直斜面向下时,滑块乙静止,
对甲有:mgsinα=ma1
从A到B,由运动学公式得:
| v | 2 1 |
甲与乙碰撞,由动量守恒定律,得:mv1=2mv
甲与乙碰撞后,以两滑块为研究对象,由牛顿第二定律,
得:μF′N-2mgsinα=(m+m)a2
即??μ(2Eq+2mgcosα)-2mgsinα=2ma2
从B到C由运动学公式,得:
| v | 2 2 |
联解得:μ=
| 15 |
| 32 |
即要使甲、乙不能到C点,须有μ>0.47
答:为使它们不能到达C点,滑块与斜面间的动摩擦因数大于0.47.
点评:该题考查了牛顿第二定律、运动学公式、动量守恒定律等多个知识点,关键要清楚物体的运动过程,根据题目情景条件列出相应的等式.

练习册系列答案
相关题目