题目内容
某同学在研究性学习中，利用所学的知识解决了如下问题：一轻弹簧一端固定于某一深度为h=0.25m，且开口向右的小筒中（没有外力作用时弹簧的下部分位于筒内），如图甲所示，如果本实验的长度测量工具只能测量出距筒口右端弹簧的长度l，现要测出弹簧的原长l0和弹簧的劲度系数，该同学通过改变挂砝码的个数来改变l，作出F-l变化的图线如图乙所示．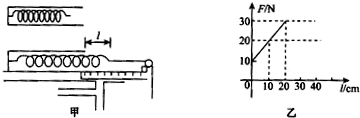
（1）由此图线可得出的结论是
（2）弹簧的劲度系数为
（1）由此图线可得出的结论是
在弹性限度内，弹力与弹簧的伸长量成正比
在弹性限度内，弹力与弹簧的伸长量成正比
．（2）弹簧的劲度系数为
100
100
N/m，弹簧的原长l0=0.15
0.15
m．分析：（1）在弹性限度内，弹力和弹簧的伸长量成正比．
（2）根据胡克定律写出F与l的关系式，然后结合数学知识求解即可．
（2）根据胡克定律写出F与l的关系式，然后结合数学知识求解即可．
解答：解：（1）根据图象结合数学知识可知：在弹性限度内，弹力与弹簧的伸长量成正比．
故答案为：在弹性限度内，弹力与弹簧的伸长量成正比．
（2）设弹簧原长为l0，则根据胡克定律有：F=k（h-l0+l）=kl+k（h-l0）
由此可知，图象的斜率大小表示劲度系数大小，故：k=100N/m，
当l=0时，F=10N，将数据代入方程①可解得：l0=15cm．
故答案为：100，15．
故答案为：在弹性限度内，弹力与弹簧的伸长量成正比．
（2）设弹簧原长为l0，则根据胡克定律有：F=k（h-l0+l）=kl+k（h-l0）
由此可知，图象的斜率大小表示劲度系数大小，故：k=100N/m，
当l=0时，F=10N，将数据代入方程①可解得：l0=15cm．
故答案为：100，15．
点评：找到各个物理量之间的关系，然后根据胡克定律列方程，是解答本题的突破口，这要求学生有较强的数学推导能力．
练习册系列答案
相关题目
某同学在研究性学习中，利用所学的知识解决了如下问题：一轻弹簧竖直悬挂于某一深度为h=25.0cm，且开口向下的小筒中（没有外力作用时弹簧的下部分位于筒内，但测力计可以同弹簧的下端接触），如图（甲）所示，如果本实验的长度测量工具只能测量出筒的下端弹簧的长度l，现要测出弹簧的原长l0和弹簧的劲度系数，该同学通过改变l而测出对应的弹力F，作出F-l变化的图线如图（乙）所示．，则弹簧的劲度系数为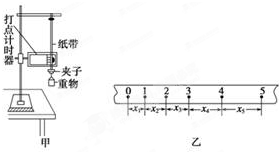
某同学在研究性学习中充分利用打点计时器针对自由落体运动进行了如下三个问题的深入研究：
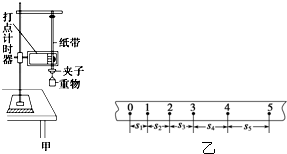某同学在研究性学习中充分利用打点计时器针对自由落体运动进行了如下三个问题的深入研究：
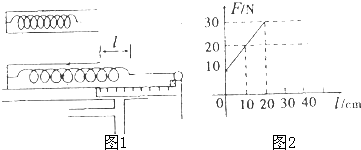某同学在研究性学习中，利用所学的知识解决了如下问题：一轻弹簧一端固定于某一深度为h=0.25m、且开口向右的小筒中（没有外力作用时弹簧的下部分位于筒内），如图1所示，如果本实验的长度测量工具只能测量出距筒口右端弹簧的长度l，现要测出弹簧的原长l0和弹簧的劲度系数，该同学通过改变挂钩码的个数来改变l，作出F-l变化的图线如图2所示．