题目内容
 轻绳一端系在质量为M=30kg的物体A上,另一端系在一个质量为m=2kg套在粗糙竖直杆MN的圆环上.现用水平力F拉住绳子上一点,使物体A从如图所示实线位置O缓慢下降到虚线位置O′、θ=53°时,圆环恰好要下滑,取sin37°=0.6,cos37°=0.8.则杆与环间动摩擦因数μ为( )
轻绳一端系在质量为M=30kg的物体A上,另一端系在一个质量为m=2kg套在粗糙竖直杆MN的圆环上.现用水平力F拉住绳子上一点,使物体A从如图所示实线位置O缓慢下降到虚线位置O′、θ=53°时,圆环恰好要下滑,取sin37°=0.6,cos37°=0.8.则杆与环间动摩擦因数μ为( )分析:物体A到虚线位置O′时,圆环恰好要下滑,说明圆环受到的静摩擦力达到最大值,先以整体为研究对象,求出杆对圆环的静摩擦力,再以结点O′为研究对象,分析受力情况,根据平衡求出拉力F,即可得到杆对圆环的弹力,由f=μN求解μ.
解答:解:以A和圆环及绳组成的整体为研究对象,分析受力情况,如图1,由平衡条件得
f=(M+m)g
N=F
再以结点O′为研究对象,分析受力情况,如图2,则由平衡条件得
F=Mgtan53°
又由题意,物体A到虚线位置O′时,圆环恰好要下滑,圆环受到的静摩擦力f达到最大值,则有f=μN
代入得到,μ=
=0.8
故选D

f=(M+m)g
N=F
再以结点O′为研究对象,分析受力情况,如图2,则由平衡条件得
F=Mgtan53°
又由题意,物体A到虚线位置O′时,圆环恰好要下滑,圆环受到的静摩擦力f达到最大值,则有f=μN
代入得到,μ=
| M+m |
| Mtan53° |
故选D
点评:本题一要掌握物体间刚要发生相对滑动时,静摩擦力达到最大值,二灵活选择研究对象,采用整体法和隔离法相结合的方法,比较简便.

练习册系列答案
相关题目
 (2012?徐州一模)轻绳一端系在质量为m的物体A上,另一端系在一个套在粗糙竖直杆MN的圆环上.现用水平力F拉住绳子上一点O,使物体A从图中实线位置缓慢下降到虚线位置,但圆环仍保持在原来位置不动.则在这一过程中,环对杆的摩擦力F1和环对杆的压力F2的变化情况是( )
(2012?徐州一模)轻绳一端系在质量为m的物体A上,另一端系在一个套在粗糙竖直杆MN的圆环上.现用水平力F拉住绳子上一点O,使物体A从图中实线位置缓慢下降到虚线位置,但圆环仍保持在原来位置不动.则在这一过程中,环对杆的摩擦力F1和环对杆的压力F2的变化情况是( )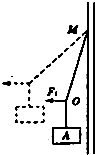 如图所示轻绳一端系在质量为m的物体A上,另一端系在竖直杆的M点上,现用水平力F1拉住轻绳上的一点O,使物体A从图中实线位置缓慢上升到虚线位置,在这一过程中,水平力F1和绳OM的拉力F2的变化是( )
如图所示轻绳一端系在质量为m的物体A上,另一端系在竖直杆的M点上,现用水平力F1拉住轻绳上的一点O,使物体A从图中实线位置缓慢上升到虚线位置,在这一过程中,水平力F1和绳OM的拉力F2的变化是( ) 如图所示,轻绳一端系在质量为m的物体A上,另一端与套在粗糙竖直杆MN上的轻圆环B相连接.现用水平力F拉住绳子上一点O,使物体A及圆环B静止在图中虚线所在的位置.现稍微增加力F使O点缓慢地移到实线所示的位置,这一过程中圆环B仍保持在原来位置不动.则此过程中,圆环对杆摩擦力F1
如图所示,轻绳一端系在质量为m的物体A上,另一端与套在粗糙竖直杆MN上的轻圆环B相连接.现用水平力F拉住绳子上一点O,使物体A及圆环B静止在图中虚线所在的位置.现稍微增加力F使O点缓慢地移到实线所示的位置,这一过程中圆环B仍保持在原来位置不动.则此过程中,圆环对杆摩擦力F1 轻绳一端系在质量为m的物体A上,另一端系在一个套在倾斜粗糙杆MN的圆环上.现用平行于杆的力F拉住绳子上一点O,使物体A从图中实线位置缓慢上升到虚线位置,并且圆环仍保持在原来位置不动.则在这一过程中.环对杆的摩擦力Ff和环对杆的压力FN的变化情况是( )
轻绳一端系在质量为m的物体A上,另一端系在一个套在倾斜粗糙杆MN的圆环上.现用平行于杆的力F拉住绳子上一点O,使物体A从图中实线位置缓慢上升到虚线位置,并且圆环仍保持在原来位置不动.则在这一过程中.环对杆的摩擦力Ff和环对杆的压力FN的变化情况是( )